Integer Arithmetic
Integer의 표현은 크게 2가지가 있다.
Signed integer의 표현에는 여러 방법이 있지만, 표준으로 정의된 방법은 없다.
그러나 2의 보수가 ALU을 구현하는데 추가적인 보정이 필요 없기 때문에 누구나 다 2의 보수를 음수 표현에 사용한다.
- Unsigned integer
- 표현되는 모든 수는 양수이다.
- 표현 방법이 한가지이다.
- Signed integer
- Sign magnitude
- MSB를 부호로 사용하고, 양의 수에서 MSB가 1이면 부호만 바뀐다.
- 예 : 001 = +1, 101 = -1
- 문제점
- 양수 + 음수가 0이 되지 않는다.
- 따라서 연산에서 보정이 필요하기 때문에 ALU에서는 부적합하다.
- 1's complement
- 1의 보수를 음수로 사용한다.
- 예 : 000 = +0, 111 = -0, 100 = -3
- 문제점
- 양수 + 음수가 0이 되지 않는다.
- 따라서 연산에서 보정이 필요하기 때문에 ALU에서는 부적합하다.
- 2's complement
- 2의 보수를 음수로 사용한다.
- 양수 + 음수 = 0이 되기 때문에 ALU에서 음수 표현을 위해 사용된다.
- Biased notation
- 중간 어딘가를 0으로 기준삼는다.
- 예
- Bias 3인 경우 3의 이진법인 011을 0으로 삼는다.
- 011 = 0, 010 = -1, 001 = -2, 100 = +1, 101 = +2
- Sign magnitude
Integer Add/Sub의 문제
Integer의 덧셈에서는 carry가 발생한다.
Unsigned integer의 빼기에서는 borrow가 발생한다.
Signed integer의 빼기에서는 carry가 발생한다.
Signed integer의 빼기는 2의 보수로 변환하여 덧셈을 수행하기 때문이다.
정리하면 다음과 같다.
- unsigned number
- 덧셈 : carry 발생
- 뺄셈 : borrow 발생
- signed number
- 덧셈 : carry 발생
- 뺄셈 : carry 발생
Carry나 borrow로 인해 overflow가 발생할 수 있다.
Overflow란 연산 결과가 표현 가능한 bit 수를 넘어서는 것을 말한다.
Unsigned Arithmetic
Unsigned arithmetic에서 발생한 carry나 borrow가 의미없을 수도 있다.
예를 들어 address arithmetic은 음수라는 개념이 없기 때문에 발생한 carry와 borrow는 무시한다고 전제한다.
따라서 address arithmetic에서의 carry나 borrow는 의미가 없다.
반면, 순수한 arithmetic인 경우, overflow가 발생하면 계산 결과가 완전히 달라진다.
예를 들어, 192 + 65 = 1100 0000 + 0100 0001 = (1) 0000 0001 -> 0000 0001 = 1가 되어버린다.(carry가 발생했기 때문)
또한, 128 - 192 = (1) 1000 0000 - 1100 0000 = 1100 0000 = 192가 되어버린다.(borrow가 발생했기 때문)
Unsigned arithmetic에서 carry나 borrow로 인해 발생하는 overflow는 programmer의 책임이다.
따라서 보정에 processor가 개입하지 않는다.
프로그래머는 이를 위해, carry bit이나 borrow가 생기는지 확인하고, 생긴다면 error handling을 해야 한다.
그러나 이를 매번 하기에는 번거롭기 때문에, 충분히 큰 크기의 data type을 사용한다.
Signed Airthmetic
Signed integer에서 발생하는 overflow는 2가지 경우만 존재한다.
만약 양수 + 음수라면 값이 작아지기 때문에 overflow는 발생하지 않는다.
- 양수 + 양수
- 마지막에 발생한 2개의 carry가 01
- 음수 + 음수
- 마지막에 발생한 2개의 carry가 10

그런데 이 경우는 XOR gate을 이용해서 detect 할 수 있다.
* XOR gate : (0, 0) = 0, (0, 1) = 1, (1, 0) = 1, (1, 1) = 0
Overflow에 대해 프로그래머가 책임진다면, 프로그래머는 overflow가 발생하는지 확인하고, 발생할 경우 error handling을 해야 한다.
이는 unsigned arithmetic과 마찬가지이고, 이렇게되면 하드웨어는 모든 연산에 개입을 하지 않는 consistency를 가진다.
그런데 signed arithmetic에서 발생하는 overflow는 항상 에러이다.(ignore case가 없음)
따라서 processor가 개입하여 보정을 할 수도 있다.
이는 high-level language 마다 다르고, 따라서 두 종류의 instruction set을 구현해야 한다.
MIPS Arithmetic Instruction Set
두 종류의 arithmetic instruction을 제공한다.
- processor 개입 X
- overflow를 ignore한다.
- addu, addiu, subu
- "u"의 의미는 unsigned가 아닌, "overflow를 무시한다."는 의미이다.
- processor 개입 O
- overflow을 detect한다.
- overflow가 발생하면 exception handler를 호출한다.
- EPC(Exception Program Counter) register에 현재 PC 값을 저장한다.
- 미리 정의된 handler address로 jump하여 execption handler를 수행한다.
- overflow는 bug와 마찬가지이기 때문에 execption handler는 process를 stop하고 crash 시킨다.
- overflow가 발생하면 exception handler를 호출한다.
- add, addi, sub
- overflow을 detect한다.
C는 모든 것을 프로그래머가 책임지도록 하기 때문에 add, addi, sub 등만 사용한다.
Fortran은 signed number에 대해서는 add, addi 등을 이용하고, unsigned number에 대해서는 addu, addiu, subu 등을 사용한다.
매우 큰 수의 integer 표현
Interger를 표현하는 bit 수는 한정되어 있기 때문에 매우 큰 수를 표현하기 위해서는 다음과 같은 방법을 이용한다.
- double precision : 더 큰 data type 사용
- floating point : not integer type, 그러나 더 큰 수 표현 가능
Integer Multi/Divide의 문제
Integer multiplication은 add에 비해 훨씬 느리고, 많은 공간을 필요로 한다.
Integer division은 multiplication에 비해 느리다.
Integer Multiplication
Integer multiplication은 shift와 더하기를 반복해서 수행한다.
Negative number는 양수로 변환하여 곱셈을 수행한다.
두 수의 곱의 결과의 bit 수는 두 수의 bit 수의 합과 동일하다.
따라서 곱셈은 많은 시간과 많은 공간을 필요로 한다.

Multiplication을 더 빠르게 구현하기 위해서 하드웨어를 충분히 사용한다.
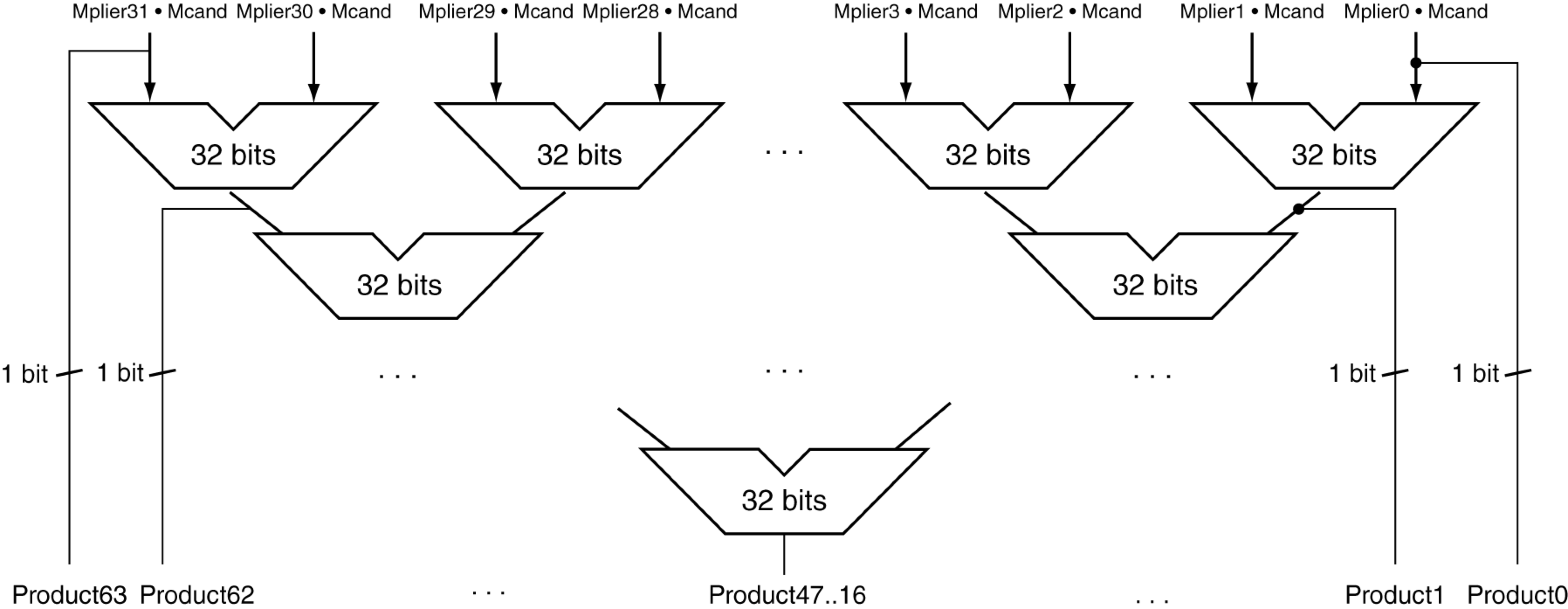
32bit * 32bit는 총 32개의 덧셈을 수행하게 된다.
따라서 미리 그 32개의 중간 결과를 구한 후에 2개씩 더하는 연산을 반복한다.
이러한 방법이 moore's law에 따라 반도체 기술이 증가함에도 불구하고 CPU의 크기가 커지는 이유 중 하나이다.
MIPS Multiplication
32bit * 32bit는 64bit의 결과를 만들어낸다.
따라서 2개의 공간에 나눠서 저장해야 한다.
이를 위해 MIPS는 HI와 LO의 레지스터를 제공한다.
- HI : 연산 결과의 최상단의 32개 bit를 저장한다.
- LO : 연산 결과의 최하단의 32개 bit를 저장한다.
이를 이용하여 다음과 같은 instruction들을 제공한다.
- multi rs, rt / multu rs, rt
- HI/LO에 64bit 결과를 나눠서 저장한다.
- mfhi rd / mflo rd
- HI/LO register로부터 rd에 값을 옮긴다.
- mul rd, rs, rt
- rs * rt의 최하단 32bit을 rd에 저장한다.
- 연산 결과가 충분히 작아서 32bit로 표현 가능할 때 사용한다.
Integer Division
Integer division은 multiplication을 여러번 반복해서 수행한다.
따라서 integer multiplication에 비해 느리다.

MIPS Division
MIPS는 division 몫과 나머지를 담기 위해 HI와 LO register를 사용한다.
- HI : 연산결과 중 나머지(reminder)을 저장한다.
- LO : 연산결과 중 몫(quotient)을 저장한다.
이를 이용하여 MIPS는 다음과 같은 instruction을 제공한다.
- div rs, rt / divu rs, rt
- rs와 rt를 나눈 결과를 HI/LO에 저장한다.
- mfhi rd / mflo rd
- HI/LO의 결과를 rd에 저장한다.
Overflow나 0으로 나누는 것에 대해 점검하지 않기 때문에 프로그래머가 책임져야 한다.
'Computer Science > Computer Architecture' 카테고리의 다른 글
| 3. Multimedia Arithmetic (0) | 2021.05.16 |
|---|---|
| 3. Floating-Point Arithmetic (0) | 2021.05.16 |
| 3. Computer Arithmetic (0) | 2021.05.16 |
| 2. Compile, Link, Run (0) | 2021.05.09 |
| 2. MIPS : Runtime Environment (0) | 2021.05.09 |





댓글