Batch Normalization
Input을 normalization을 하는 것이 아닌 중간의 것을 normalization 한다.
Normalization Target : a vs. z
a(비선형변환의 결과)를 normalization하지 않고 z(선형변환의 결과)를 normalization 한다.
방법
Mini-batch의 z에 대해 normalization을 수행한다.
Mini-batch에 m 개의 sample이 존재한다고 하자.(mini-batch size = m)
평균과 분산을 구해서 그것을 이용해서 normalization을 한다.
아래를 이용해서 $z^{[l](i)}$ 대신에 $\widetilde{z}^{[l](i)}$을 사용한다.
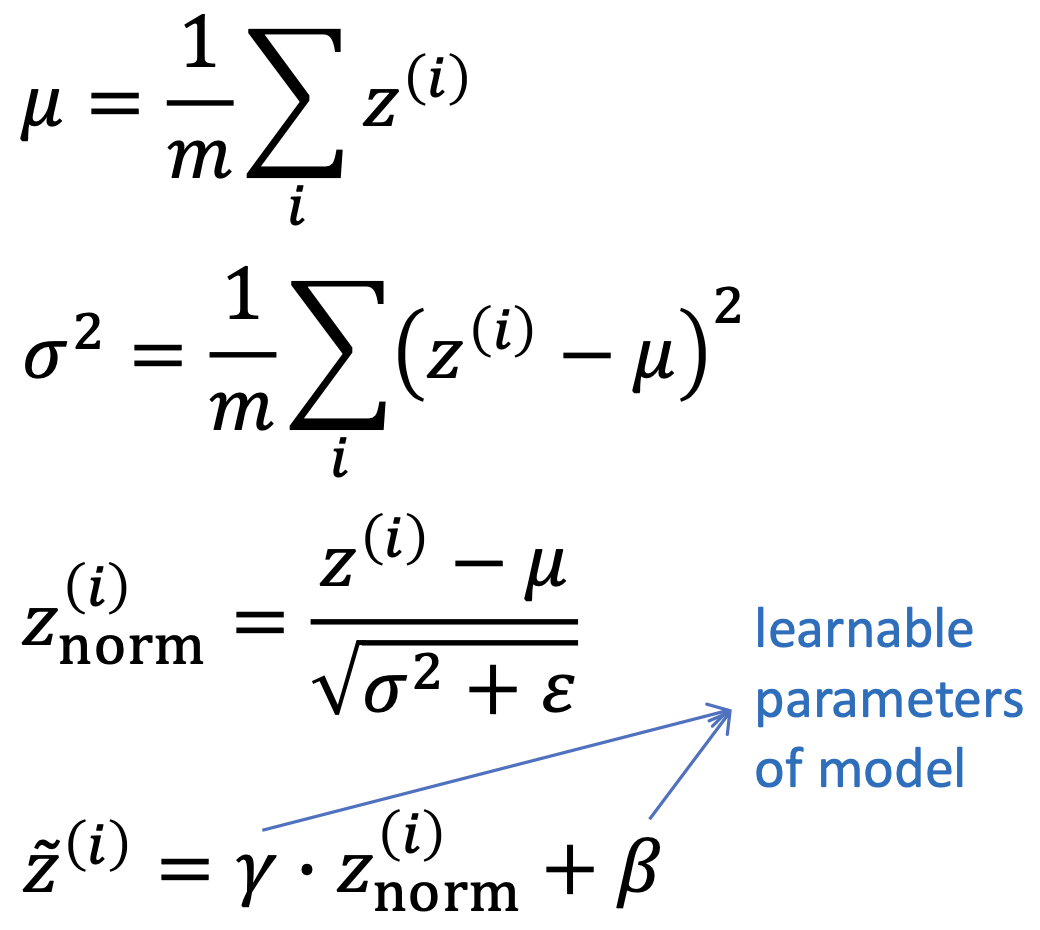
Parameter $\beta$, $\gamma$
$z_{norm}^{(i)}$을 하면 평균은 0, 분산은 1이 된다.(정규분포 형태)
이 평균과 분산이 최적의 값인지는 모르기 때문에 learnable parameter를 두어 최적의 값을 찾도록 한다.
$\beta$와 $\gamma$는 learnable parameter이기 때문에 hyperparameter가 아니다.
모델에서 normalization이 필요 없다고 판단하면 $\gamma = \sqrt{\sigma ^2 + \epsilon}$, $\beta = \mu$가 된다.
이 때 $\widetilde{z}^{(i)} = z^{(i)}$가 된다.
특징
- learning speed를 높일 수 있다.
- input layer의 value를 normalization하는 것이 아니라 hidden unit의 input에 normalization 한다.
- Mini-batch에 대해 적용한다. (mini-batch의 평균과 분산을 이용해서 normalization 한다.)
장점
- 많은 조합의 hyperparameter가 잘 동작하도록 해준다.
- Hyperparameter search problem을 쉽게 만들어준다.
- Neural network가 hyperparameter의 선택에서 좀 더 robust하도록 한다.
- Deep network가 훈련이 잘 되도록 해준다.
Batch Normalization to Network
결과를 내는데 방해가 될 수 있기 때문에 output layer에는 normalization을 적용하지 않는다.
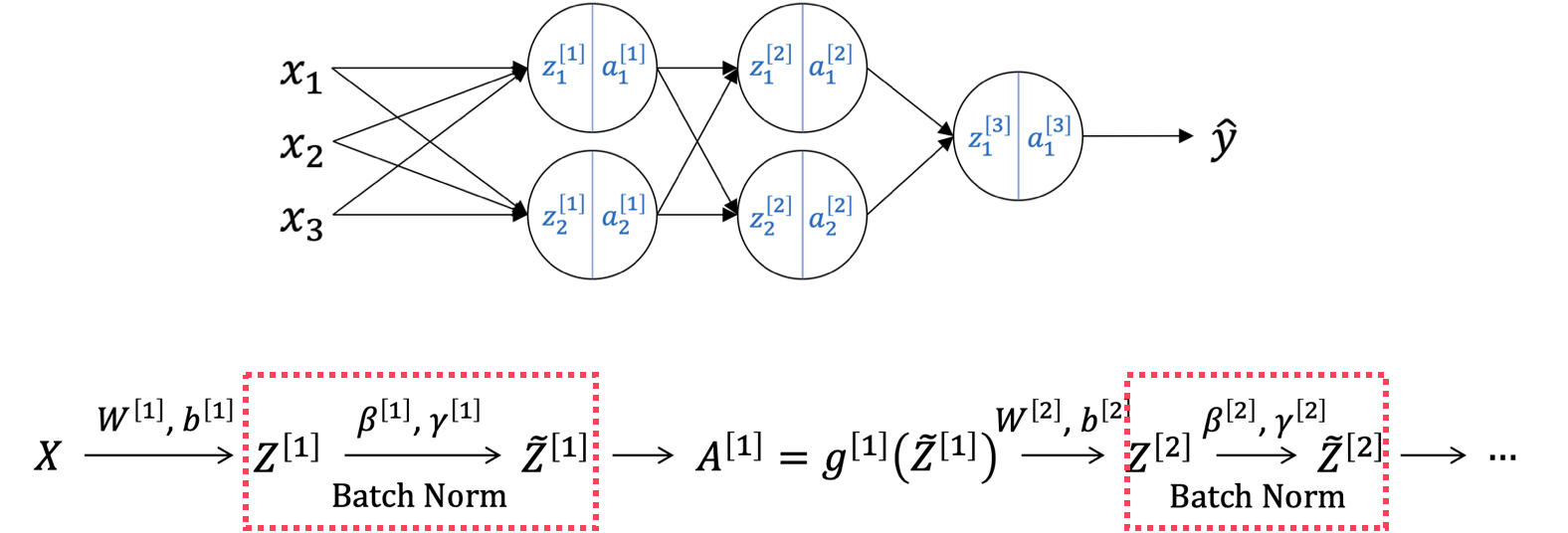
Parameter $b$의 제거
Batch normalization은 z에 normalization을 하는 것이고 learnable parameter $\gamma$와 $\beta$를 같이 사용한다.
때문에 $z = Wa + b$에서의 b는 batch normalization의 $\beta$와 역할이 같기 때문에 의미가 사라진다.
따라서 계산 cost를 줄이기 위해서 b를 생략한다.
이 때의 parameter는 $w$, $\gamma$, $\beta$가 된다.

Batch Normlization at Test Time
Training에서 batch normalization을 하였으면 test 시에도 batch normalization을 해야 한다.
문제
Test set의 sample은 많지 않다.
이로 인해 mini-batch 안에도 충분한 sample이 존재하지 않는다.
따라서 평균과 분산을 구하기 힘들어진다.
해결
Training에서 사용된 여러 개의 $\mu$와 $\sigma$를 모아서 그들의 평균된 버전(혹은 exponentially weighted average)을 사용한다. (마지막, 그 앞에 등등)
'Computer Science > AL, ML' 카테고리의 다른 글
| Optimization (0) | 2022.04.21 |
|---|---|
| [Batch Normalization] Covariate Shift Problem (0) | 2022.04.21 |
| Batch, Mini-batch (0) | 2022.04.21 |
| Normalization (0) | 2022.04.20 |
| Weight Initialization - Gradient Problem 방지 (0) | 2022.04.20 |





댓글