Bayesian Classification
특징
- statistical classifier
- bayes theorem에 기반을 둔 statistical classifier이다.
- Probabilistic prediction을 수행한다.(확률적으로 예측을 한다.)
- comparable performance
- Naive bayesian classifier는 decision tree나 neural network에 대해 comparable한 성능을 보인다.
- Incremental
- 미리 mining한 knowledge가 새로 들어온 정보에 의해 찾아진 knowledge와 쉽게 combine될 수 있다.
- scratch에서 다시 training하는 것보다 combine하는 것이 훨씬 빠르다.
Bayesian Theorem
- evidence
- = target data sample
- class label을 모르는 data sample이다.
- hypothetis : "data sample X가 class C에 속한다."는 명제
- classification : $P(H \vert X)$
- $P(H \vert X)$ : X가 주어질 때 X가 C에 속할 확률
- $P(H \vert X)$를 통해 classification을 수행한다.
- $P(H \vert X)$는 조건부 확률을 이용하여 구한다.
- priori probability : $P(H)$
- 사전 확률 : X가 주어지기 전의 확률
- X와 관계 없이 H가 일어날 확률
- X에 대해 independent하다.
- class 별로 주어진다.
- evidence : $P(X)$
- X가 존재할 확률
- sample data X가 존재할 확률
- posteriori probabiltiy : $P(X \vert H)$
- 사후 확률, 조건부 확률
- class C에서 X가 발견될 확률
장단점
- 장점
- easy to implement : 확률만 구하면 된다.
- 대부분의 경우에서 괜찮은 결과를 낳는다.
- 단점
- assumption
- attribute간 depedency가 존재할 수 있음에도 불구하고 conditional independent라고 가정한다.
- 이로 인해 accuracy가 떨어질 수 있다.
- dependency는 naive bayesian classifier로 모델링 할 수 없다.
- assumption
Classification
X의 class는 $P(C_i | X)$가 가장 큰 class $C_k$로 한다.
따라서 P(H|X) 구함을 통해 classification을 수행한다.
P(H|X)는 아래와 같이 조건부 확률을 통해 구할 수 있다.

이는 아래와 같이 표현할 수 있다.
likelihood = posteriori * priori / evidence
증명
$P(H|X) = \frac{P(H \cap X)}{P(X)}$
$P(X|H) = \frac{P(H \cap X)}{P(H)}$
$\Rightarrow P(H \cap X) = P(H|X)P(X) = P(X|H)P(H)$
$\Rightarrow P(H|X) = P(X|H)P(H) / P(X)$
Conditionally Independent
각 class에 대해 조건부확률을 구하기는 힘드므로 attribute 간에는 독립적이라고 가정한다.
이를 conditionally independent라고 한다.
따라서 $P(X|C_i)$는 각 sample $x_k$와 class $C_i$의 조건부 확률의 곱으로 계산할 수 있다.
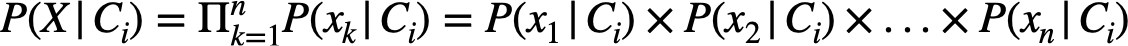
이를 통해 computation cost를 상당히 줄일 수 있다.
Categorical vs. Continuous-Valued Attribute
Categorical attribute에 대해서는 $C_i$에 속하는 tuple들 중에 $A_k$라는 attribute가 $x_k$인 tuple들의 개수를 구하면 된다.
Continuous-valued attribute에 대해서는 정규분포를 따른다고 가정하고 평균과 표준편차를 계산해서 아래와 같은 수식으로 대체할 수 있다.

예시

0-Probability Problem
$P(H|X) = P(X|H) \times P(H)$
$P(X|C_i) = \Pi ^n _{k=1} P(x_k | C_i)$
이기 때문에 $P(x_k | C_i)$ 중 하나라도 0이 되면 전체가 0이 되는 문제가 발생한다.
해결 방법 : Laplacian Correction(Estimator)
각 case에 대해서 1을 더해서 0이 되지 않도록 방지한다.
아래에서 분모가 1000이 아닌 1003임에 주의하자.
- P(income = low) = 0/1000 → 1/1003
- P(income = medium) = 990 / 1000 → 991/1003
- P(income = high) = 10 / 1000 → 11 / 1003
'Computer Science > Data Science' 카테고리의 다른 글
| [Classification] Associative Classification (0) | 2022.04.18 |
|---|---|
| [Classification] Rule-based Classification (0) | 2022.04.18 |
| [Decision Tree] Gini Index (0) | 2022.04.18 |
| [Decision Tree] Gain Ratio (0) | 2022.04.18 |
| [Decision Tree] Information Gain (0) | 2022.04.18 |





댓글