Constraint-Based Mining (Query-Directed Mining)
제약조건(constraint)이 있을 때의 association rule mining 방법이다.
Constraint-based Mining
사용자가 원하는 constraints를 주고 system이 mining을 수행한다.
- user flexibility : mining하고 싶은 constraints를 제공한다.
- system optimization : 전달받은 constraints에 대해서 효율적으로 mining을 수행한다.
Data Mining에서 Constraints의 종류
- Knowledge type constraint
- 어떤 종류의 mining을 할 것인가
- classification, association, clustering 등
- Data constraint
- 데이터에 대한 제약 조건을 두고 mining을 수행
- like SQL query
- 예 : ~~한 ~~ 학생
- Dimension/level constraint
- attribute(dimension)에 대한 constraint
- 어떤 attribute를 고려할 것인가
- Interestingness constraint
- 유용함의 기준을 어떻게 둘 것인가
- minimum support, minimum confidence 등에 대한 조건
Constraint Pushing
Constraint-based mining 시 constraint를 일찍 처리(pushing)해서 탐색하는 경우를 줄인다.
Pushing 가능한 경우는 아래 3가지이다.
- Anti-monotonicity : itemset S가 조건을 만족하지 못하면 그의 superset도 조건을 만족하지 못함
- Monotonicity : itemset S가 조건을 만족하면 그의 superset도 조건을 만족함
- Succinctness
- 조건을 만족하는 하나의 itemset만 보더라도 간단한 계산을 통해 조건을 만족하는 모든 itemset을 알 수 있음
- 일부를 보고 간단하게 전체를 알 수 있음
다른 Operation과의 비교
vs. Autonomously Mining
- Autonomously mining
- 자동으로 database에서 모든 조건에 대한 pattern을 찾는 것은 비현실적이고 바람직하지 않다.
- pattern의 수가 너무 많기 때문
- 사용자가 원하는 것에 초점이 맞춰져 있지 않음
- 자동으로 database에서 모든 조건에 대한 pattern을 찾는 것은 비현실적이고 바람직하지 않다.
- Constraint-based mining
- data mining query language 사용
- 사용자가 mining하기 원하는 것을 전달할 수 있음
- interactive process 제공
- data mining query language 사용
vs. Constraint-based Search
- 공통점 : 모든 것이 대상이 아니라 일부만 대상으로 탐색을 수행
- 차이점
- constrained mining : 조건에 해당하는 모든 패턴을 산출
- constraint-based search : AI 등을 통해 조건에 해당하는 일부 또는 하나의 답만을 산출
vs. Query Processing in DBMS
- 공통점 : 조건에 해당하는 모든 답을 산출
- 차이점
- constrained mining : 숨겨진 패턴을 발견해냄
- query processing : 그저 DB 안에 있는 tuple을 반환
Constraint Pushing
Constraint-based mining 시 constraint가 아래 조건 중 하나이면 constraint을 빠르게 처리할 수 있다.
아래 경우에 대해서면 constraint를 만족하지 않은 것을 바로바로 제거하면서 mining하면 된다.
- Anti-monotonicity
- Monotonicity
- Succintness
Anti-Monotonicity
Itemset S가 조건을 만족하지 못하면 S의 superset도 조건을 만족하지 못한다.
$sum(S.price) \leq v$ 은 anti-monotone이다.
price는 항상 양수이므로 더 할 수록 값이 커져서 한번 조건을 위배하면 그의 superset도 위배하기 때문이다.
반면, $sum(S.price) \geq v$는 anti-monotone이 아니다.
Monotonicity
Itemset S가 조건을 만족하면 S의 superset도 조건을 만족한다.
$sum(S.price) \geq v$이나 $min(S.price) \leq v$는 monotone하다.
이미 S의 최솟값이 $v$보다 작다면 $v$보다 큰 요소가 들어와도 min은 $v$이고 $v$보다 작은 요소가 들어오면 min은 $v$보다 작아지기 때문이다.
Succintness
Constraint를 만족하는 일부의 itemset만 보더라도 간단한 계산을 통해 모든 itemset을 유추해낼 수 있다.
일부만 보고 간단한 계산을 통해 전체를 알 수 있는 경우이다.
좋은 succient constraint는 transaction DB를 보지 않고도 itemset S가 만족하는지 알 수 있는 조건이다.
$min(S.price) \leq v$는 succint하다.
price가 $v$보다 작은 item과 다른 item들의 모든 조합들이 전체 itemsets이기 때문이다.
그러나 $sum(S.price) \geq v$는 succint하지 않다.
조건이 여러 개 있으며 간단한 연산을 통해 유추해낼 수 없기 때문이다.
예시
아래에서 볼 수 있듯이 빠르게 pruning을 하여 mining을 efficient하게 만든다.
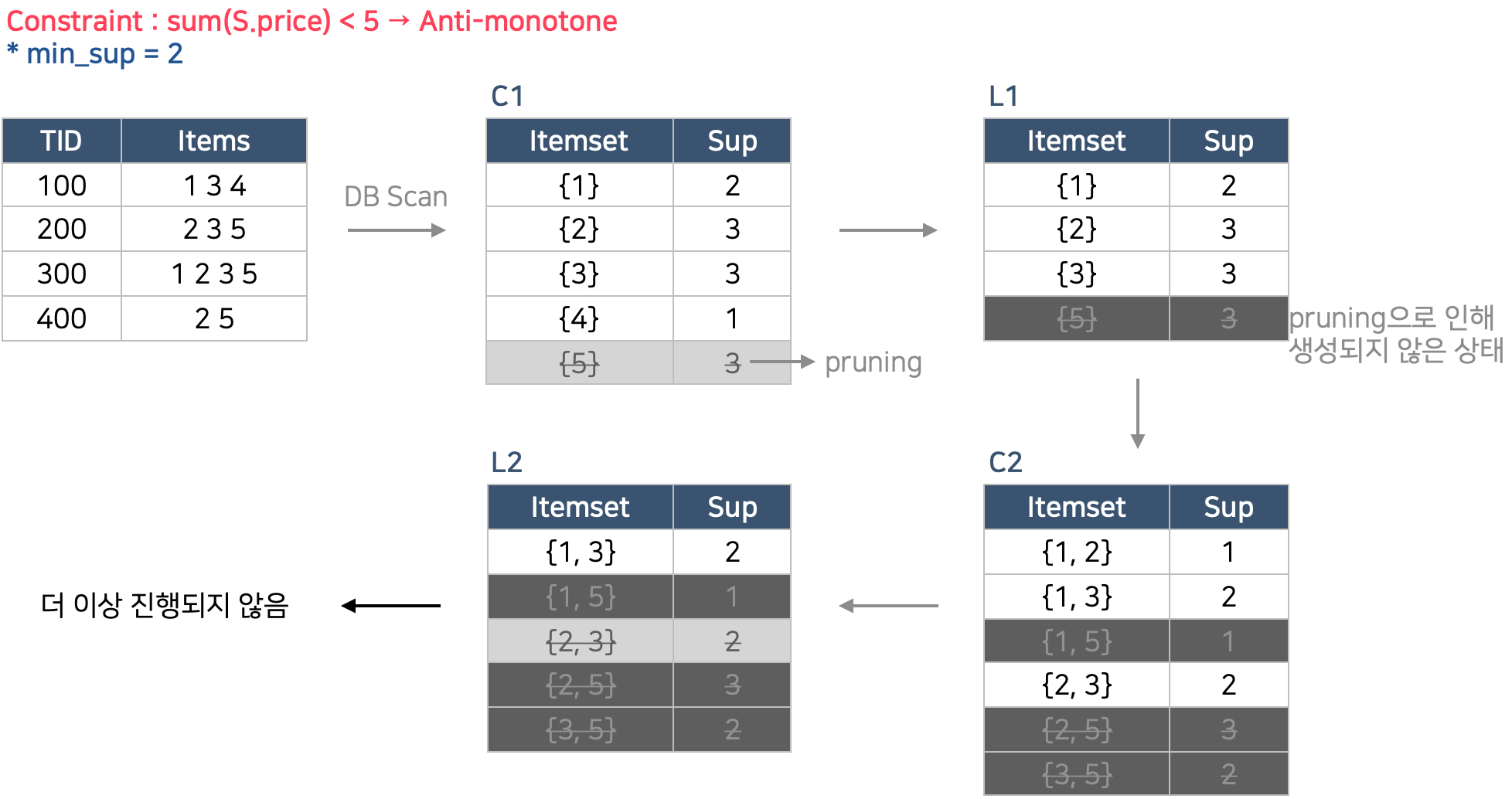
Tough한 경우
anti-monotone/monotone/succint하지 않은 것을 tough하다 한다.
Tough한 경우에는 약간의 트릭을 부려서 anti-monotone/monotone하게 만들 수 있다.
Ordering을 이용한다.
예를 들어 $avg(S.profit) \geq 25$는 tough cosntraint이다.
이런 경우 value를 내림차순으로 정렬해서 anti-monotone하게 만들 수 있다.
더 작은 요소가 들어오면 평균이 더 작아지므로 내림차순으로 정렬하면 anti-monotone하게 된다.
'Computer Science > Data Science' 카테고리의 다른 글
| Classification/Prediction에 대한 여러가지 Issues (0) | 2022.04.18 |
|---|---|
| Classification, Prediction (0) | 2022.04.18 |
| Correlations (Lift) (0) | 2022.04.17 |
| Quantitative Association Mining (0) | 2022.04.17 |
| Multi-level Association, Multi-dimensional Association (0) | 2022.04.17 |





댓글