Information Gain
더 높은 information gain 값을 가지는 attribute를 test attribute로 사용한다.
Entropy
Entropy는 heterogeneous한 정도, 즉 혼잡도를 의미한다.
Entropy의 값이 높을 수록 heterogeneous하고, 작을 수록 homogeneous함을 의미한다.
Entropy = $Info(D) = -\Sigma ^m _{i=1} p_i log_2 p_i$
$m$ : class의 수
Attribute A로 나눈 후의 data set D의 entropy는 아래와 같다.
이 때 나눠지는 sample들의 개수를 고려해야 하므로 그 비율을 곱한다.
$Info_A(D) = \Sigma ^v _{j=1} \frac{\vert D_j \vert}{\vert D \vert} \times Info(D_j)$
$v$ : A로 나눴을 때 나눠진 partition의 개수
Information Gain
Attribute로 나눈 후의 entropy의 값이 작을수록 homogenous 해짐을 의미하는 것이므로, 아래 information gain 값이 커지는 것이 유리함을 의미한다.
같은 dataset에 대해서 어떤 attribute로 나눌지를 비교할 때에는 $Info(D)$의 값이 동일하므로 $Info_A(D)$의 값이 작아지는 A를 선택하면 된다.
Information Gain = $Gain(A) = Info(D) - Info_A (D)$
Continuous-Value Attribute
Continuous-valued attribute인 경우 split point를 정해서 discrete하게 바꾸고 information gain을 적용한다.
어떤 split point가 좋을지에 대해서는 각각에 대해 나눴을 때의 information gain을 계산해서 정한다.
Minimum entropy(max info gain)를 가지는 split point가 best split point이다.
해당 split point에 대해 binary하게 나누어 decision tree를 형성한다.
여러 개의 split point를 정해서 여러 덩어리로 나눌 수는 있다.
그러나 이는 조합이 너무 많기 때문에 cost가 크다.
따라서 하나의 split point에 대해 binary하게 나누는 것이 보통이다. (practical)
예시
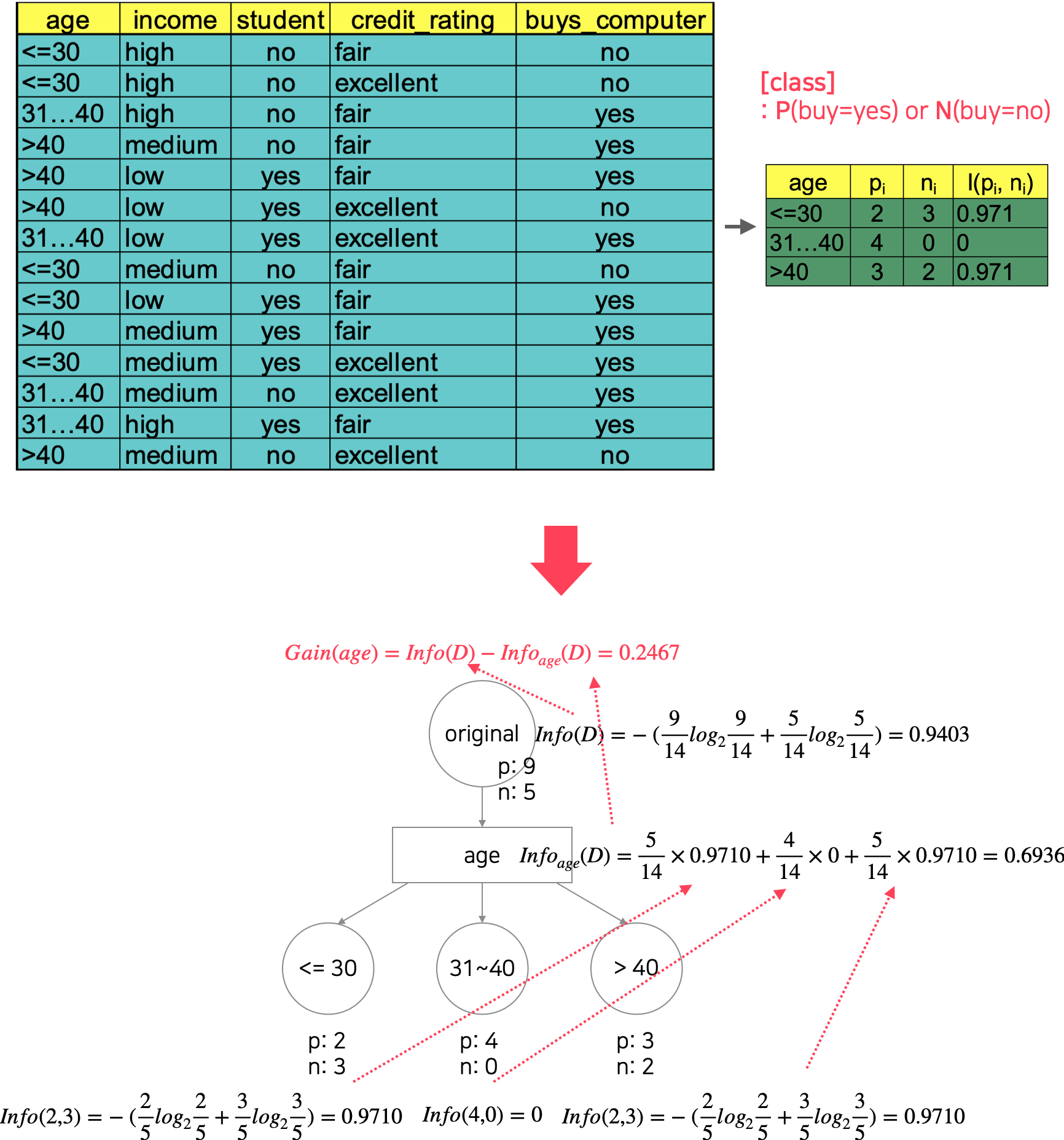
위 방식대로 수행하면,
- age : $Info_{age} = 0.6936 \rightarrow Gain(age) = 0.2467$
- <= 30 : 0.9710
- 31~40 : 0
- > 40 : 0.9710
- income : $Info_{income} = 0.9143 \rightarrow Gain(income) = 0.026$
- low : 0.8113
- medium : 0.9183
- high : 0.8113
- student : $Info_{student} = 0.7885 \rightarrow Gain(student) = 0.1518$
- yes : 0.5917
- no : 0.9852
- credit_rating : $Info_{credit\_rating} = 0.8922$
- fair : 0.8113
- excellent : 1
이 된다.
따라서 age로 나눴을 때의 entropy가 가장 작고 $Info(D)$의 값은 공통이므로 Gain값은 age로 나눴을 때 가장 작다.
첫번째 test attribute는 age가 되어야 한다.
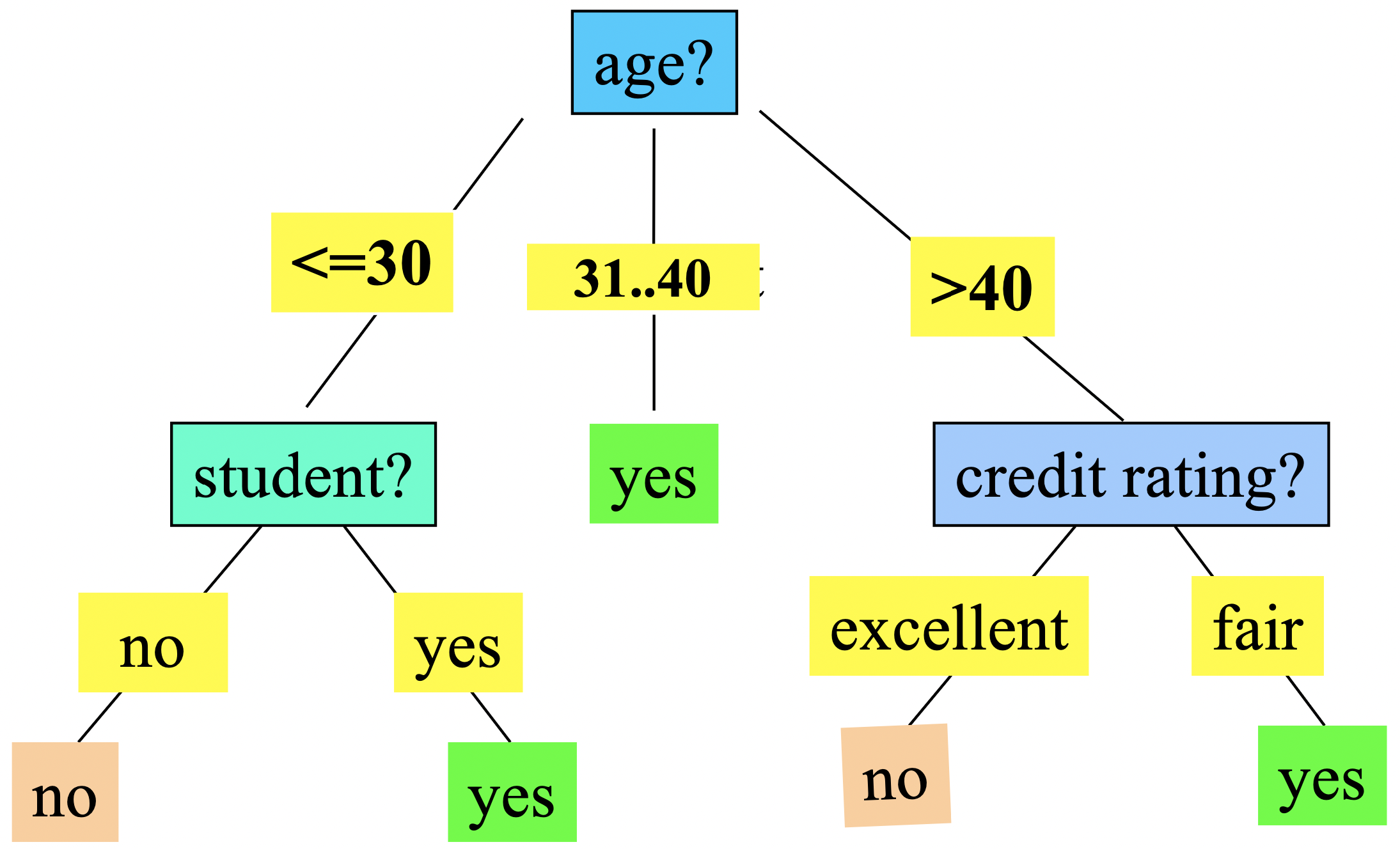
위 과정을 recursive하게 leaf까지 수행해나가면 아래와 같은 decision tree가 생성된다.
'Computer Science > Data Science' 카테고리의 다른 글
| [Decision Tree] Gini Index (0) | 2022.04.18 |
|---|---|
| [Decision Tree] Gain Ratio (0) | 2022.04.18 |
| [Classification] Decision Tree (0) | 2022.04.18 |
| Classification/Prediction에 대한 여러가지 Issues (0) | 2022.04.18 |
| Classification, Prediction (0) | 2022.04.18 |





댓글