Logistic Regression
입력값이 주어졌을 때 정답일 확률을 예측하는 방법으로, 주로 binary classification을 위해 사용된다.
하나의 unit으로 이루어진 네트워크 형태를 가진다.
입력값 x에 대해 $y=1$일 확률을 잘 추론해낼 수 있는 $w$와 $b$를 찾아야 한다.
Model
선형변환 → 비선형변환
- Parameter : 우리가 찾아야 하는 값
- $w \in R^{n_x}$
- $b \in R$
- Output : 연산 수행 결과
- 입력값 x에 대해 y=1일 확률을 구한다.
- $\hat{y} = \sigma(w^T x + b)$
- $w^Tx + b$ : linear transformation(affine transformation)
- $\sigma(z)$ : non-linear transformation, 주로 sigmoid 사용
Matrix를 이용해서 아래처럼 표현하기도 한다.
$x' = \begin{bmatrix} 1 \\ x \end{bmatrix}, x' \in R^{n_x+1}$
$\theta = \begin{bmatrix} \theta_0 \\ \theta_1 \\ ... \\ \theta_{n_x} \\ \end{bmatrix}$ ($\theta_0 = b$)
$\Rightarrow \hat{y} = \sigma(\theta ^T x')$
Parameter
Unknown variable로 우리가 찾기 위해 training 하는 값이다.
비선형 변환 쪽에 존재하지 않고, 선형 변환 쪽에 존재한다.
Output
선형변환 + 비선형변환을 수행한 값이다.
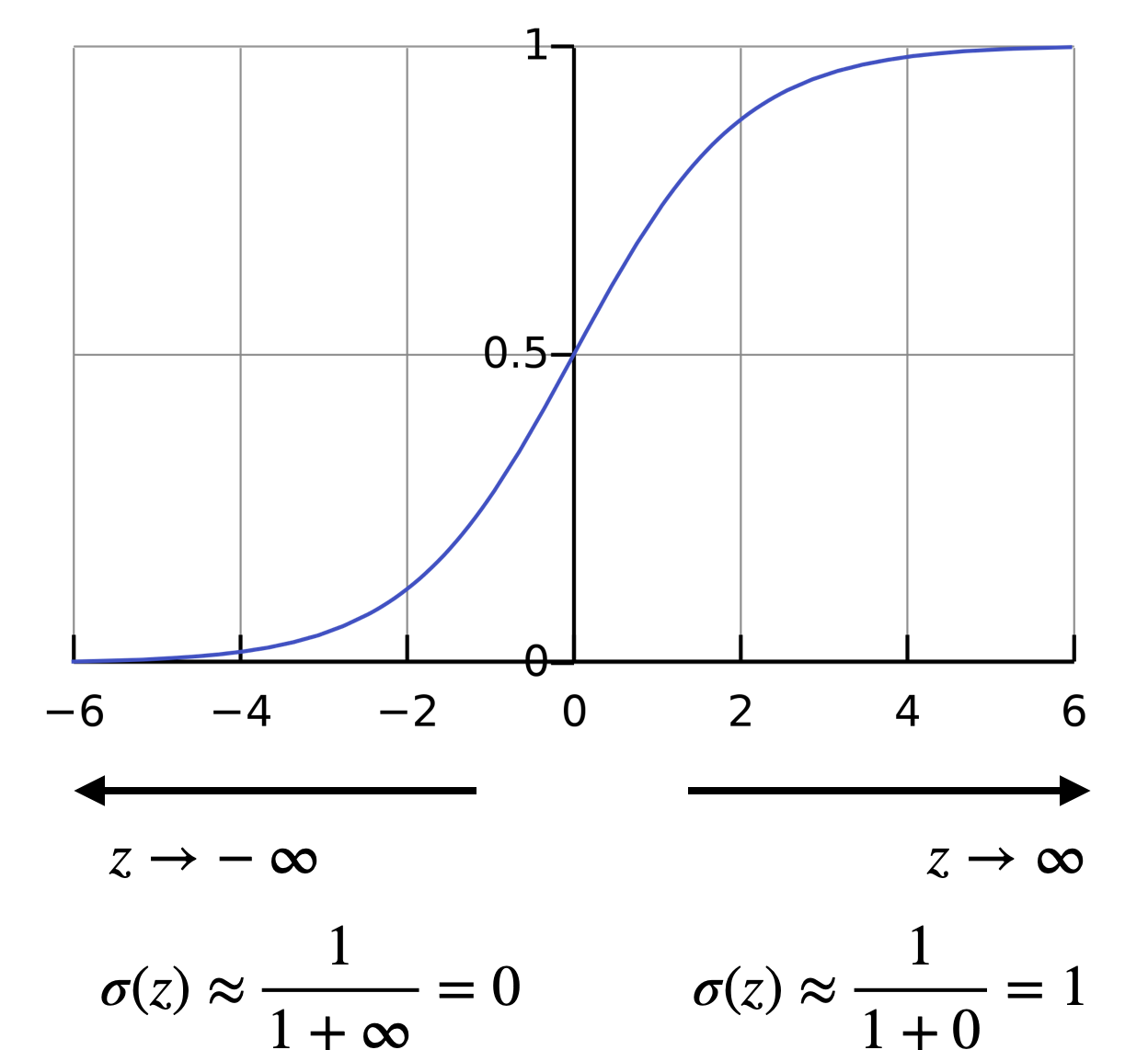
비선형 변환으로 주로 sigmoid를 사용한다.
$\sigma(z) = \frac{1}{1 + e^{-z}}$
Loss Function, Cost Function
Euclidean loss는 classification task에서 vanishing gradient 문제를 야기할 수 있어서 주로 cross-entropy loss를 사용한다.
* Cross-entropy loss : $L(\hat{y}, y) = -(ylog\hat{y} + (1-y)log(1- \hat{y}))$
따라서 cost function은 $J(w, b) = -\frac{1}{m} \Sigma ^m _{i=1} [ y^{(i)}log\hat{y}^{(i)} + (1-y^{(i)}) log ( 1-\hat{y}^{i} ) ]$ 가 된다.
Gradient Descent
Gradient descent를 통해 $J(w, b)$를 최소화하는 $w$와 $b$를 찾는 것이 training의 목표이다.
컴퓨터가 gradient를 쉽게 계산하기 위해서 computation graph를 이용하여 수식을 만들 수 있다.
Gradient
Computation graph를 이용해서 gradient를 계산할 수 있다.
아래와 같은 모델에서
- $x$ : input
- $z = w^Tx + b$ : linear/affine function
- $\hat{y} = a = \sigma(z)$ : nonlinear function, output
- $L(a, y) = -(yloga + (1-y)log(1-a))$ : loss function for one sample

따라서 아래와 같은 결과를 얻을 수 있다.
$dw_1 = \frac{dL(a, y)}{dw_1} = \frac{dL}{dz} \cdot \frac{dz}{dw_1} = x_1 \cdot dz = x1 \cdot (a-y)$
$dw_2 = \frac{dL(a, y)}{dw_2} = \frac{dL}{dz} \cdot \frac{dz}{dw_2} = x_2 \cdot dz = x2 \cdot (a-y)$
$db = \frac{dL(a, y)}{db} = \frac{dL}{dz} \cdot \frac{dz}{db} = dz = a-y$
위 수식을 이용해서 gradient descent alogorithm에서
- $w_1 \leftarrow w_1 - \alpha \cdot dw_1$
- $w_2 \leftarrow w_2 - \alpha \cdot dw_2$
- $b \leftarrow b - a \cdot db$
를 통해 $w_1, w_2, b$의 값을 수렴해간다. 여기에서 $\alpha$는 learning rate를 의미한다.
여러 sample에 적용
여러 개의 sample에서 loss는 각 sample에 대한 loss의 평균을 사용한다.
$J(w, b) = \frac{1}{m} \Sigma ^m _{i=1} L(a^{(i)}, y^{(i)})$
따라서 derivate도 각 input에 대한 derivate의 평균으로 사용하면 된다.
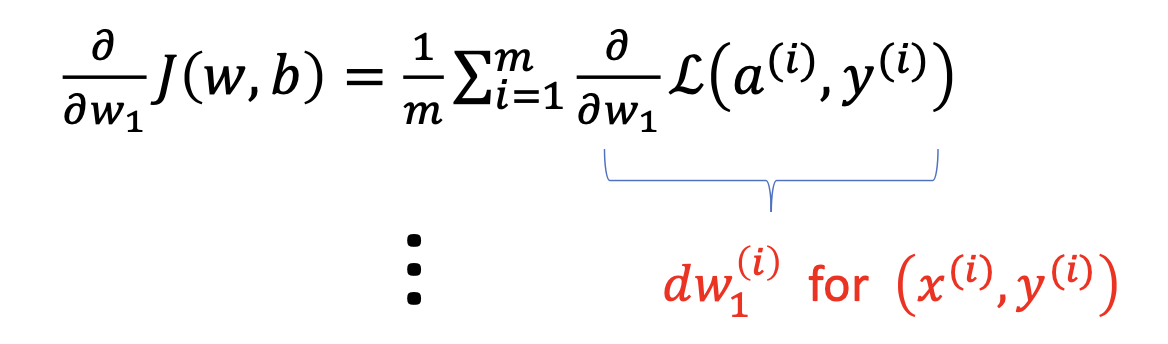
Pseudo Code
이 과정을 수도코드로 작성해보면 아래와 같다.
# Initialize
w1 = 1, w2 = 0.5, b = 1
J = 0, dw1 = 0, dw2 = 0, db = 0
for iter in range(1000): # 학습횟수
for i = 1 to m:
# Forward propagation
z[i] = w.T * x[i] + b
a[i] = sigmoid(z[i])
# loss
J += -(y[i]*log(a[i]) + (1-y[i])*log(1-a[i]))
# Backward propagation
dz[i] = a[i] - y[i]
dw1 += x[i][1] * dz[i]
dw2 += x[i][2] * dz[i]
db += dz[i]
# Average
J /= m, dw1 /= m, dw2 /= m, db /= m
w1 = w1 - l * dw1
w2 = w2 - l * dw2
b = b - l * db
Vectorization
Vectorization은 for loop를 크게 줄임으로써 연산 속도를 높이는 과정이다.
Python에서는 numpy를 통해 vectorizing 할 수 있다.
Numpy는 GPU나 CPU의 parallelization instruction(SIMD) 을 통해 연산 속도를 높인다.
* SIMD : Single Instruction Multiple Data
때문에 numpy를 통해 지원되는 연산이 있다면 for loop와 math를 이용한 연산보다는 numpy에서 지원되는 메소드를 통해 수행하는 것이 좋다.
위 과정을 vectorization하면 아래와 같다.
# Initialize
J = 0, dw1 = 0, dw2 = 0, db = 0
for iter in ragne(1000): # 학습횟수 -> 제거 불가
# for i = 1 to m:
# Forward propagation
Z = np.dot(w.T, X) + b # z[i] = w.T * x[i] + b
A = sigmoid(Z) # a[i] = sigmoid(z[i])
# Backward propagation
dZ = A - Y # dz[i] = a[i] - y[i]
dW = np.dot(X, dZ.T)/m # dw1 += x[i][1] * dz[i]
# dw2 += x[i][2] * dz[i]
db = np.sum(dZ)/m # db += dz[i]
# Average
# J /= m, dw1 /= m, dw2 /= m, db /= m
w -= l * dw
b -= l * db
'Computer Science > AL, ML' 카테고리의 다른 글
| Gradient Descent of Neural Network (0) | 2022.04.09 |
|---|---|
| Neural Network (0) | 2022.04.07 |
| Computation Graph (Forward/Backward Propagation) (0) | 2022.04.06 |
| Gradient Descent (0) | 2021.08.06 |
| Loss Function, Cost Function (0) | 2021.08.06 |





댓글