Activation Function
Non-linear function, identity function 이라고도 한다.
Sigmoid 외에도 많은 non-linear function이 존재한다.
그러나 어떤 함수를 activation function으로 사용하기 위해서는 그 함수의 gradient를 구할 수 있어야 한다.
즉, 미분 가능한 함수여야 한다.
단, ReLU는 한 점에서 미분 불가능하지만 practical하게 문제가 거의 발생하지 않기 때문에 사용 가능한 함수도 존재한다.
Vanishing Gradient
함수의 기울기(gradient)가 0이거나 0에 가까워지면 variable이 update 되지 않게 된다.
이를 해결하기 위해서는 모든 부분에서 gradient가 예쁘게 나오는 함수를 사용해야한다.
그러나 이는 또다른 문제를 야기할 수 있기 때문에 요즘에는 practical하게 문제가 발생하지 않는 ReLU를 사용한다.
Activation Function으로 Non-linear을 사용하는 이유
Linear function을 여러 번 사용하여도 결국 하나의 linear function으로 표현할 수 있다.
즉, activation function으로 linear function을 사용한다면 아무리 많은 layer를 쌓더라도 neural network는 결국 단순한 linear function의 결과를 나타낸다.
한번의 선형변환 만으로는 중요한 정보가 나오지 않기 때문에 이는 의미 없는 행동이 된다.
때문에 non-linear activation function이 사용되어야 한다.
여러가지 함수들
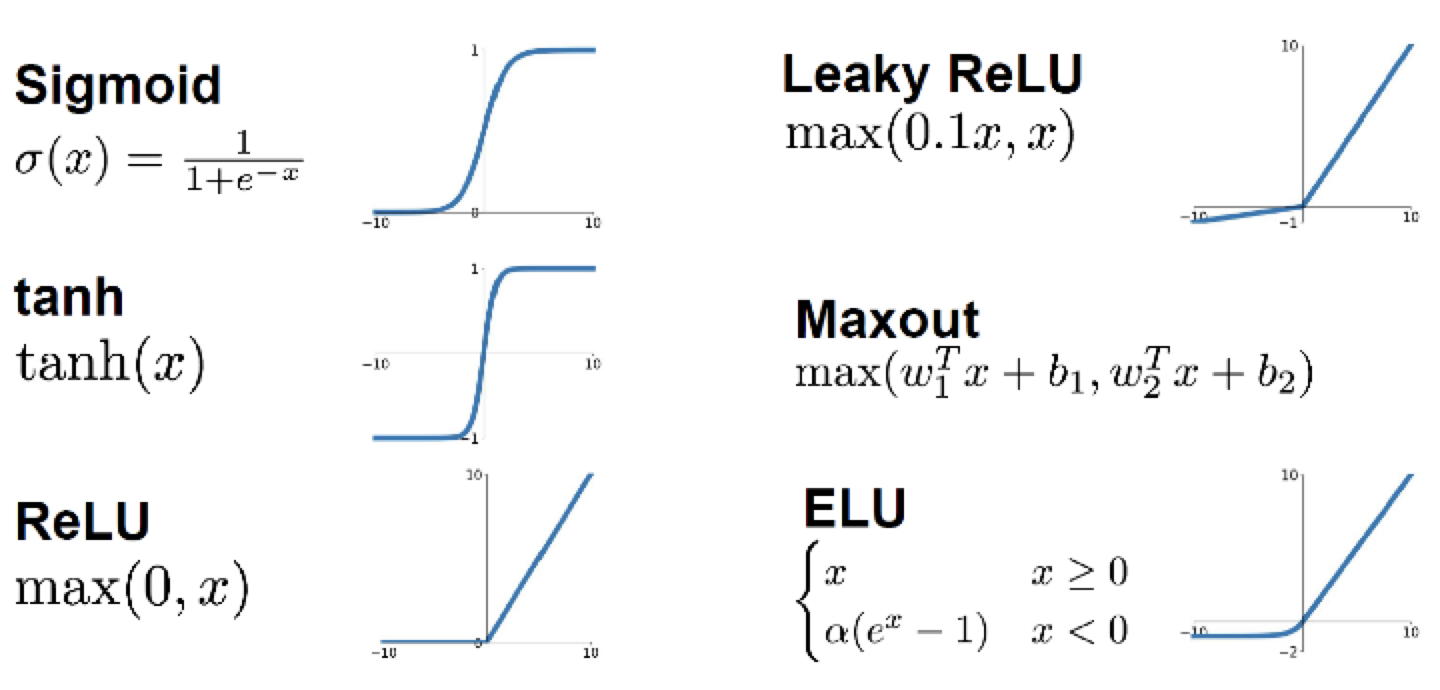
Sigmoid
Sigmoid는 여러 문제가 존재하기 때문에 확률을 나타내기 위해 output layer에 사용되는 경우 외에는 거의 사용되지 않는다.
0~1 사이의 값을 갖는다.
$g(z) : \sigma = \frac{1}{1 + e^{-z}}$
$g'(z) = g(z)(1-g(z))$

문제점
- exp 계산은 cost가 높다.
- 양끝으로 가면 vanishing gradient 문제가 발생한다.
- output이 zero-centered 되어 있지 않고 항상 positive하다. → undesired zig-zag dynamics를 야기한다.
Zig-zag Convergence
$f = \Sigma w_i x_i + b$이므로 $\frac{df}{dw_i} = x_i$ 이다.
따라서 $\frac{dL}{dw_i} = \frac{dL}{df} \frac{df}{dw_i} = \frac{dL}{df} x_i$ 가 된다.
모든 input $x_i$가 양수라고 가정하면 $df$는 scalar이기 때문에 모든 $dw_i$의 부호는 같다.
어떤 $w$는 양수, 어떤 $w$는 음수가 나오고 update가 되며 수렴해가야 되는데 모든 $w$의 부호가 같아지기 때문에 비효율적으로 돌아서 수렴하게 된다.
아래 그림과 같이 zig-zag path를 따라 수렴하게 되는 것이다.
이는 매우 비효율적이고 속도가 느리기 때문에 문제이다.

Hyperboic Tangent (tanh)
-1~1 사이의 값을 갖는다.
Sigmoid function이 수학적으로 변형된 방법이다.
항상 sigmoid보다 성능은 좋지만 cost가 더 높다.
Output이 zero-centered 되어이씩 때문에 zig-zag 문제가 발생하지 않는다.
양 끝으로 갈수록 기울기가 매우 작아져서 여전히 vanishing gradient 문제가 발생한다.
$g(z) : a = \frac{e^z - e^{-z}}{e^z + e^{-z}}$
$g'(z) : 1-g(z)^2$

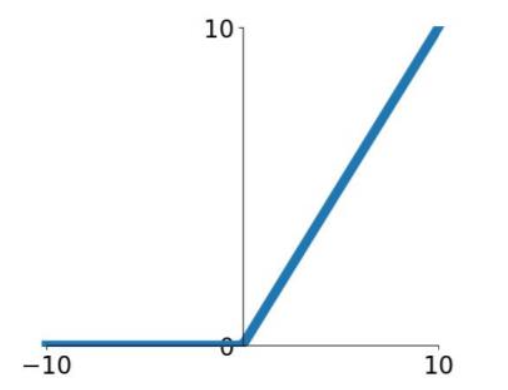
ReLU (Rectified Linear Unit)
$g(z) : a = max(0, z)$
$\Rightarrow a = \left \{ \begin{matrix} 0 \; (z \leq 0) \\ z \; (z > 0) \end{matrix} \right.$
$g'(z) = \left \{ \begin{matrix} 0 \; (z \leq 0) \\ 1 \; (z > 0) \end{matrix} \right.$
ReLU(Rectified Linear Unit)은 의미없는 값을 정리하는 기능으로 생각할 수 있다.
쓸모없는 신호는 꺼보리고 의미있는 정보만 버리는 셈이다.
ReLU를 사용하면 쓸모없는 정보를 음수로 보내는 w와 b를 찾게 된다.
Vanishing gradient problem이 존재하지 않는다고 볼 수 있다.
원점은 잘 나오지 않으며 원점에서의 gradient는 1이나 0 중에 문제에 적합하게 사용하면 된다.
확률을 산출하는 output layer 외에는 ReLU가 default choice로 사용된다.
장점
- 오른쪽 부분에 대해서 vanishing gradient problem이 발생하지 않는다.
- 계산적으로 효율적이다.
- sigmoid나 tanh보다 실질적으로 수렴이 빠르다.
- sigmoid보다 더 그럴듯 하다.
단점
- not zero-centered output
- 항상 양수인 input이 들어온다면 모든 w의 부호가 같아져서 zig-zag가 발생하게 된다.
- 그러나 계산속도가 매우 빠르고 쓸모없는 정보는 0로 차단하기 때문에 실질적으로 유용하다.
Leaky ReLU
ReLU의 변형된 버전이다.
$z \leq 0$ 일 때 0으로 만들어서 update 되지 않도록 하는 것이 아니라 아주 느리게 update가 일어나도록 한다.
Leaky ReLU가 ReLU보다 성능이 잘나오지만 ReLU 성능 정도로도 충분하기 때문에 주로 ReLU를 사용한다.
$g(z) : a = max (0.01z, z)$
$g'(z) = \left \{ \begin{matrix} 0.01 \; (z \leq 0) \\ 1 \; (z > 0) \end{matrix} \right.$

장점
- Vanishing gradient problem이 발생하지 않는다.
- 계산적으로 효율적이다.
- sigmoid나 tanh보다 실질적으로 수렴이 빠르다.
- 값을 죽이지 않는다.
Parametric Rectifier (PReLU)
ReLU/Leaky ReLU을 일반화시킨 함수이다.
$f(x) = max(\alpha x, x)$
$\alpha$ 는 trainable parameter로, $x$와 같은 shape의 trainable array이다.
따라서 $\frac{dL}{d\alpha}$도 계산해야하기 때문에 training 시 cost가 더 비싸다.
다만, 학습이 끝나면 성능이 더 좋다.
Exponential Linear Units (ELU)
Leaky ReLU와 유사하지만 $x \leq 0$ 부분에서 1차 함수를 사용하는 것이 아니라 exponential을 사용한다.
Leaky ReLU와 마찬가지의 이유로 잘 사용되지 않는다.
$f(x) = \left \{ \begin{matrix} x \; (x > 0) \\ \alpha(exp(x) - 1) \; (x \geq 0) \end{matrix} \right.$
장점
- ReLU의 모든 이점을 가지고 있다.
- 원점에서도 gradient가 0이 아니다. → gradient가 0이 되는 지점이 존재하지 않는다.
- $x$가 매우 작을 때 그에 비례해서 gradient가 매우 커지는 문제를 해결하였다.
단점
- exp를 계산하는데 cost가 발생한다.
Maxout Neuron
PReLU의 일반화된 버전이다.
Piece-wise linear의 형태를 띈다.
$f(x) = max (w_1 ^T x + b_1, w_2 ^T x + b_2)$
여기서의 $w, b$는 activation function의 parameter로 linear transformation에 사용되는 $w, b$와는 다른 것이다.
$w_1 = b_1 = 0$이면 ReLU가 된다.
장점
- Parameter를 여러 개 가지고 있기 때문에 더 좋은 성능을 가질 수 있다.
- 따라서 학습이 종료되면 더 좋은 성능을 가질 수 있다.
- 값을 죽이지 않는다.
단점
- paramters/neuron의 수가 더 많다.
- 학습 시 resource를 더 필요로 하게 된다.
'Computer Science > AL, ML' 카테고리의 다른 글
| Deep Neural Network (DNN) (0) | 2022.04.20 |
|---|---|
| XOR with Neural Network (0) | 2022.04.20 |
| Vectorization of Neural Network (0) | 2022.04.09 |
| Gradient Descent of Neural Network (0) | 2022.04.09 |
| Neural Network (0) | 2022.04.07 |





댓글