K-Means
K-means는 partitioning clustering method 중 하나이다.
각 cluster의 대표 object(seed points)로 centroid를 사용한다.
Badness function으로 각 object가 속하는 cluster의 centroid까지의 거리의 제곱 합을 이용한다.
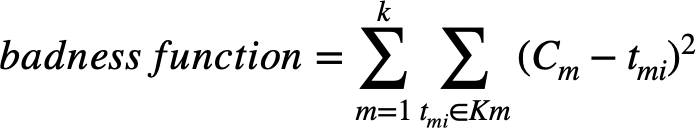
* $C_m$ : 각 cluster의 centroid
방법
- split : 임의로 k개의 subset으로 나눈다.
- seed point : 나눠진 k개의 subset에서 centroid를 계산한다.
- 계산된 centroid points가 seed point가 된다.
- centroid : 해당 cluster에 속하는 모든 point의 평균점
- reassign : 모든 object들에 대해 가장 가까운 centroid가 속하는 cluster로 재배치 한다.
- clustering의 결과가 수렴할 때 까지 2-3과정을 반복한다.
장점
K-means는 seed point로 각 cluster의 centroid를 사용하기 때문에 cost가 낮다.
즉, 상대적으로 효율적이다.
$cost = O(n \times k \times t)$
* n : 전체 object의 수
* k : cluster의 수 → 주로 작음
* t : iteration 수 → 주로 작음
대부분의 경우에서 k와 t는 n에 비해 매우 작기 때문에 cost는 n에 대해 linear하게 된다.
이는 k-means method가 scalability함을 의미한다.
* PAM : $O(k(n-k)^2)$ → $n^2$
* CLARA : $O(ks^2 + k(n-k))$ → $s$ : sampling 수 → $s^2$
단점
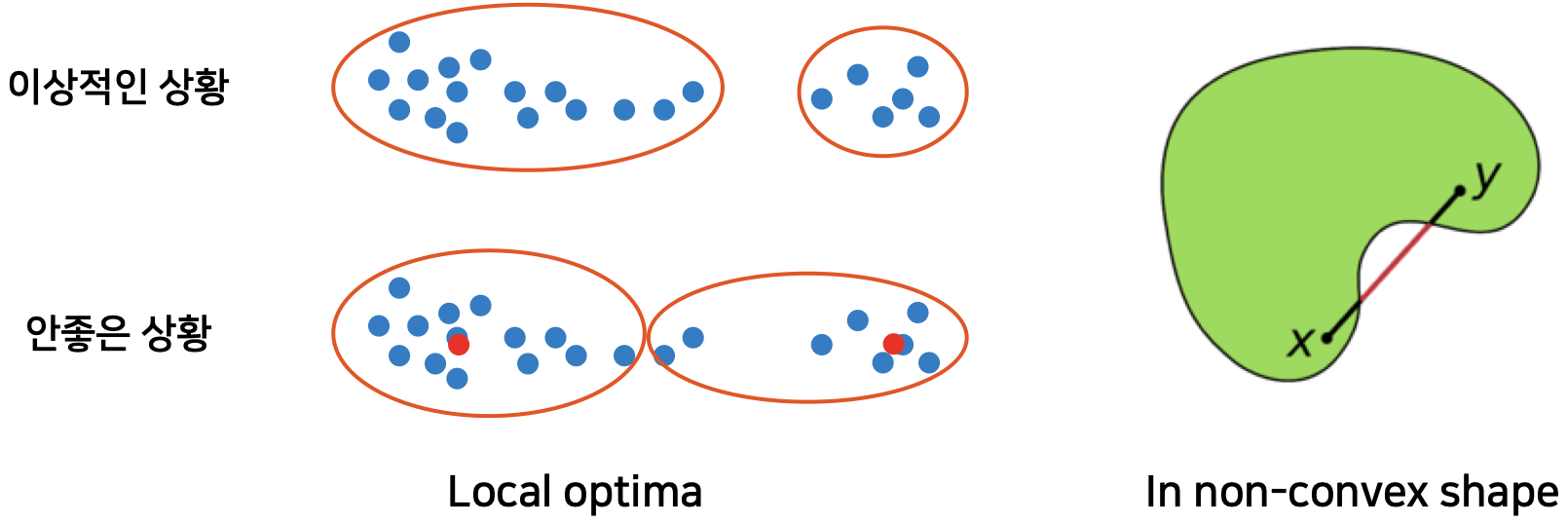
- Local optima
- Initial choice에 따라 local optima에 빠질 수 있다. (local search와 유사)
- 이를 해결하기 위해서 전체 과정을 여러 번 반복한다.
- 그러나 그럼에도 불구하고 global optima는 보장되지 않는다.
- Mean이 정의되어있어야 함
- Mean은 numerical data에 대해서만 계산이 가능하다.
- categorical data에 대해서는 변형된 방법(k-modes 등)을 이용해야 한다.
- Hyperparameter K
- K가 미리 정의되어있어야 한다.
- 어떤 k가 가장 좋은지 알 수 없다.
- Noise나 outlier에 취약하다.
- mean(평균)은 noise나 outlier에 영향을 많이 받는다.
- 때문에 seed point로 centroid를 이용하는 k-means는 noise나 outlier에 취약하다.
- Non-convex shape에 적용 불가
- 볼록하지 못한 모양에 대해서는 cluster를 찾을 수 없다.
- centroid를 기준으로 묶이기 때문에 원하는 결과가 나오지 않을 수 있다.
'Computer Science > Data Science' 카테고리의 다른 글
| [Partitioning Clustering Method] K-Medoids (0) | 2022.06.06 |
|---|---|
| [Partitioning Clustering Method] K-Modes (0) | 2022.06.06 |
| [Cluster Analysis] Partitioning Algorithm (0) | 2022.06.06 |
| [Cluster Analysis] Distance between Clusters (0) | 2022.06.05 |
| [Cluster Analysis] Measure Clustering (0) | 2022.06.05 |





댓글