Prediction
Numerical value(real-value)를 예측하는 방법이다.
대표적인 방법으로 regression이 있다.
vs. Classification
- 공통점
- Model construction → model usage의 단계를 가진다는 것에서 classification과 유사하다.
- 차이점
- Classification
- categorical class label을 예측한다.
- Prediction
- numerical value를 예측한다.
- continuous-valued function을 이용해서 continuous space에서의 value(real-value)를 예측한다.
- Classification
Regression
Predictor variable을 가지고 response variable을 예측한다.
이를 위해 하나 이상의 predictor variables와 response variable의 관계를 모델링한다.
- predictor variable(attribute)
- = independent variable
- response variable
- = dependent variable
- 예측하고자 하는 값
종류
- linear regression : 하나의 independent를 이용해서 linear한 관계를 예측
- multiple regression : 2개 이상의 independent를 이용해서 linear한 관계를 예측
- non-linear regression : non-linear한 관계를 예측
- 기타
- generalized linear model, poisson regression, log-linear models ...
Linear Regreession
하나의 independent variable과 하나의 dependent variable의 선형 관계를 예측한다.
$y = w_0 + w_1 x$
- x : single predictor variable
- y : response variable
- $w_0$ : y-intercept(y 절편)
- $w_1$ : slope (기울기)
Training
Training data를 이용해서 가장 적합한 straight line을 만드는 $w_0$와 $w_1$을 찾는다.
가장 적합한(best-fitting) 것을 찾기 위해서 error를 사용한다.
Error가 최소가 되는 것이 best-fitting이다.
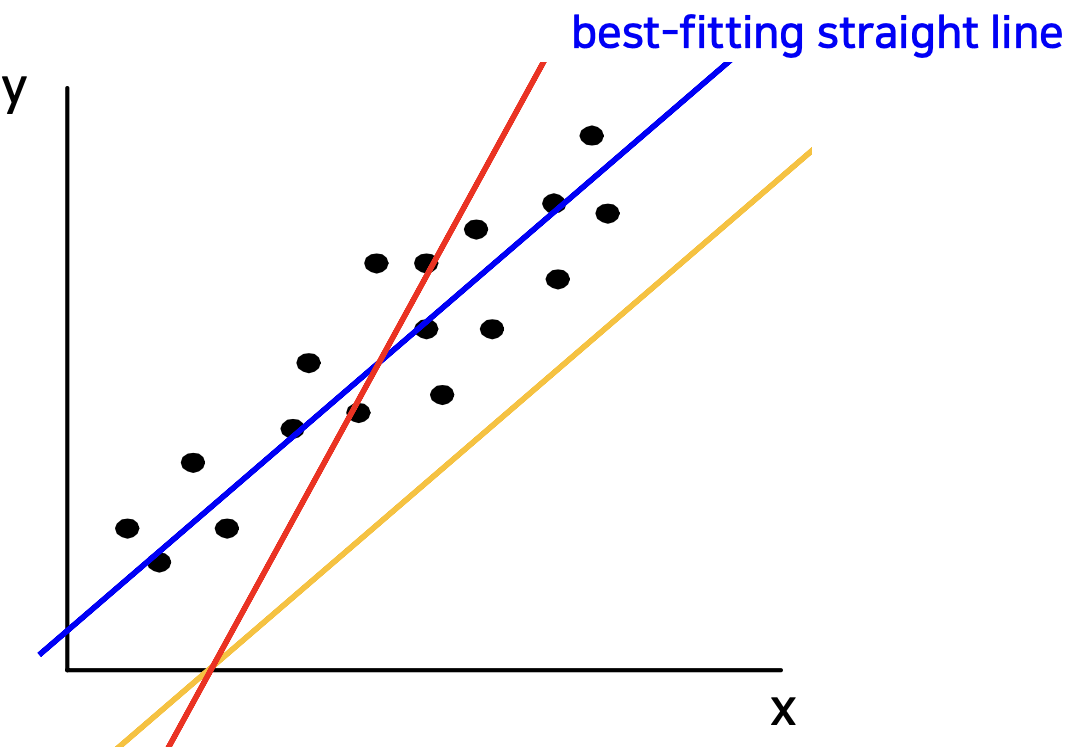
Least Squre Method
Best-fitting straight line을 찾기 위해서 least square method를 주로 사용한다.
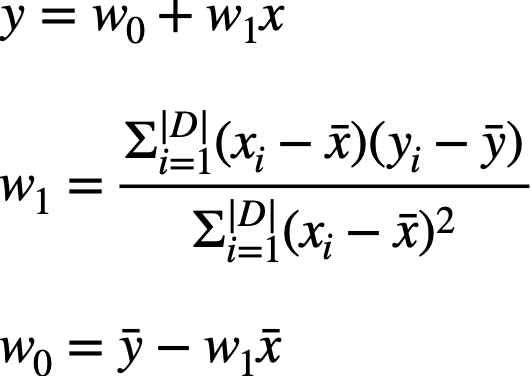
Multiple Linear Regression
2개 이사으이 independent variable과 1개의 dependent variable의 관계를 모델링한다.
X = <x_1, x_2,="" ...,="" x_n=""> 과 y의 관계를 모델링하는 것이다.
$y = w_0 + w_1 x_1 + w_2 x_2 + ...$
Least square method의 extension이나 SAS, S-Plus와 같은 툴을 이용하기도 한다.
Non-Linear Regression
Predictor와 response variable의 비선형적인 관계를 예측한다.
Polynomial function을 이용해서 공식화할 수 있다.
$y = w_0 + w_1 x + w_2 x^2 + w_ x^3$
몇차에 비례하는지 모르기 때문에 복잡하게 구현하지 않고, 주로 3차로 regression한다.
문제의 특성을 잘 알고 있어야 몇차에 비례하는지 좋은 차수를 알 수 있다.
To Linear Regression Model
Polynomial regression model은 linear regression model로 변환될 수 있다.
위 식에서 $x \rightarrow x_1$, $x^2 \rightarrow x_2$, $x^3 \rightarrow x_3$로 놓으면
$y = w_0 + w_1 x_1 + w_2 x_2 + w_3 x_3$와 같이 linear regression model로 변형시킬 수 있다.
'Computer Science > Data Science' 카테고리의 다른 글
| [Classification] Ensemble - 정확도를 높이기 위한 방법 (0) | 2022.04.18 |
|---|---|
| Classifier Accuracy Measure (0) | 2022.04.18 |
| [Classification] K-NN(K-Nearest Neighbor) Algorithm (0) | 2022.04.18 |
| Eager Learning vs. Lazy Learning (0) | 2022.04.18 |
| [Classification] Associative Classification (0) | 2022.04.18 |





댓글