컴퓨터의 탄생
아래의 발전으로 인해 컴퓨터가 탄생할 수 있었다.
- 과학적 성취 : 새로운 지식의 창조
- 19세기 George boole이 새로운 개념을 만들어 냈다.
- 실용적 도구 개발 : Automata
- 자동장치(Automata)가 개발되었다.
- 구현 기술 발전 : Transistor
- wheel(바퀴)/shfat(축)/cam, relays, 진공관을 거쳐 현재는 트렌지스터(transistor)까지 발명되었다.
- cam : 바퀴의 회전운동을 왕복운동으로 바꿔주는 장치
1. 과학적 성취 : George Boole
George Boole은 19세기 영국의 수학자이자 철학자, 논리학자이다.
≪논리와 확률의 수학적 이론의 기초가 되는 사고의 법칙 연구≫(1854)을 진행하였다.
"The Laws of Thought" (사고의 법칙)
- ≪논리와 확률의 수학적 이론의 기초가 되는 사고의 법칙 연구≫(1854)
- 논리나 추론, 철학을 수학적으로 정립한다.
- 명제(Proportions)라는 개념과 AND, OR, NOT, IF이라는 개념을 이용해 모든 것을 표현한다.
=> 인간의 논리적인 생각은 명제와 명제들을 AND, OR, NOT, IF로 결합함으로써 표현할 수 있다.
영향
- Mathematical Logic의 토대가 되었다.
- Propositional Logic(명제 논리학)으로의 토대가 되었다.
그런데 Propositional Logic은 나중에 First-order Logic (Mathemetical Logic)으로 발전하였기 때문에 결국 Mathemetical Logic의 토대가 되었다고 볼 수 있다. - Mathematical logic
- 빈틈없는 논리의 전개를 가능하게 한다.
- Knowledge-Based appoach로 AI에 접근할 수 있게 하였다.
- Propositional Logic(명제 논리학)으로의 토대가 되었다.
- Boolean Algebra의 기반이 되었다.
- Boolean algebra(부울 대수)을 통해서 Digital logic design이 가능해졌다.
- AND, OR, NOT 게이트들을 확장해나가며 CPU, memory, I/O device들을 설계할 수 있게 된 것이다.
- Computer science의 개념적인 기초를 만들어냈다고 볼 수 있다.
Propositional Logic (명제 논리)
Proposition (명제)
ture/false로 나타낼 수 있는 declarative sentence로, 변수를 포함하지 않는다.($x, a$ 등..)
예를 들어, "2 + 3 = 6"는 명제이고, "x + 3 = 5"는 명제가 아니다.
Compound Proposition
여러 proposition을 AND, OR, NOT으로 결합(compound)하여 proposition을 만든다.
결합된 proposition은 다른 proposition과 결합하여 새로운 proposition을 만든다.
예를 들어, 다음과 같은 proposition이 있다고 하자. 이를 compound하면 다음과 같다.
- $p$ : 2014.10.25 is Monday
- $q$ : $2 + 3 = 6$
- AND : p·q
- OR : p + q
- NOT : $\bar{p}$
First-order Logic
이후 First-order logic (mathemetical logic)으로 확장되었다.
여기서는 변수를 허용하기 때문에 $x + 3 = 5$도 명제가 된다.
Mathematical Logic의 영향
AI : Knowledge-Based Approach
Mathematical Logic은 Knowledge-Based appoach로 AI에 접근할 수 있게 하였다.
70년간 많은 연구와 진화가 있었고, 그를 바탕으로 Logic Programming 등이 탄생하였다.
아래 생각을 바탕으로 AI에 접근하였다.
- 사람이 intelligent한 이유는 많은 지식을 축적했고, 이로부터 논리적인 추론을 하기 때문이다.
- 그렇다면 메모리에 많은 데이터(지식)와 논리적인 추론을 담당하는 프로그램(추론)을 넣는다면 사람과 같이 생각할 수 있는 기계를 만들 것이다.
참고로, 모든 AI가 knowledge-based approach가 아니다.
- 예 : neural network(deep-learning) 등
Logic Programming
논리 문장을 이용하여 프로그램을 표현하고 계산을 수행하는 것으로, Imperative Programming과 반대된다.
* Imperative Programming (명령형 프로그래밍) : 수많은 명령문으로 구성된 것(예 : C, C++, Java 등)
예를 들어, 아래와 같은 조선시대 왕조의 족보를 만들어 보자.

이를 만들기 위해서는 다음과 같은 문장을 줘야한다.
fact (parent 세조 예종)
fact (parent 세조 의숙공주)
fact (parent 문종 단종)
fact (parent 세종 세조)
fact (parent 세종 안평대군)
fact (parent 세종 문종)
fact (parent 태종 세종)위가 입력되면 <pre>query (parent 세조 ?c)</pre>라는 물음에 [예종, 의숙공주]라는 답을 내놓을 것이다.
<pre>?c</pre>는 변수의 개념이다.
부모의 개념에 더해서 자식과 조상의 개념까지 입력을 시킨다면 다음과 같이 된다.
// 자식 개념 도입
fact (child ?c ?p) (parent ?p ?c)
// 조상 개념 도입
fact (ancestor ?a ?y) (parent ?a ?y)
fact (ancestor ?a ?y) (parent ?a ?z) (ancestor ?z ?y)<pre>(parent ?p ?c)</pre>이라면 <pre>(child ?c ?p)</pre>가 된다. 이를 통해 자식의 개념을 추가시켰다.
조상의 개념을 추가하기 위해 <pre>(parnet ?a ?y)</pre>이면 <pre>(ancestor ?a ?y)</pre>가 되도록 하였다. 그런데 부모-자식 간의 조상 개념 뿐만 아니라 부모가 아니더라도 조상이 될 수 있다. 할아버지/할머니 같은 경우이다. 따라서 그 이후 줄을 추가해줘야 한다.
<pre>(parent ?a ?z)</pre>이고 <pre>(ancestor ?z ?y)</pre>이면, <pre>(ancsetor ?a ?y)</pre>가 되도록 말이다.
이제 <pre>query (child ?c 세종)</pre>라는 물음이 가능해지고 답은 [문종, 세조, 안평대군]가 되고,
<pre>query (ancestor ?a 단종) (ancstor ?a 의숙공주)</pre>는 [태종, 세종]이 된다.
Boolean Algebra (부울 대수)
Algebra
Arithmetic은 숫자와 사칙연산을 다루는 것으로, Algebra는 arithmetic의 규칙과 변수의 개념을 사용한다.
이를 통해 숫자, 변수, 사칙연산의 관계를 방정식으로 만들 수 있다.
사용하는 value와 operation은 아래와 같다.
- value : number(숫자)
- operation : +, -, ×, ÷
Boolean Algebra
사용하는 value와 operation은 아래와 같다.
- value : {0, 1} → binary value
- operation : AND, OR, NOT
$0, 1, x_1 , x_2 , ... , x_n $와 같이 boolean expression을 통해 표현한다.
만약 $E_1 , E_2$가 boolean expression이라면, $\bar{E_1} , E_1 \cdot E_2 , E_1 + E_2$도 boolean expression이다.
2. 실용적 도구 개발 : Automata
자동장치(Automata) 의 발전
처음의 자동장치(automata)는 기계장치를 이용한 단순한 구조였다.
그러나 점점 복잡하고 정교한 자동장치를 원했고 전기가 발명되며 Digital Switch를 만들어 냈다.
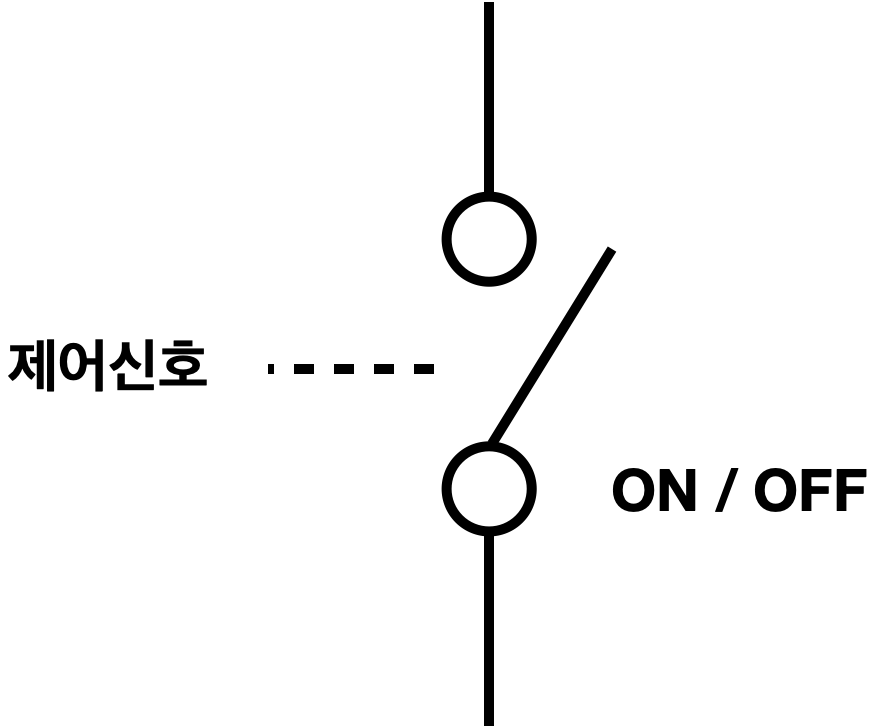
Digital Switch, Electro-Mechanical Relay
센서에 의한 신호(digital signal, control signal)를 통해 자동으로 ON/OFF를 조절하는 스위치로, 3개의 terminal로 구성되어 있다.
최초의 digital switch는 Electro-Mechanical Relay인데, 1835년 발명되어서 현재까지도 사용되고 있다.
전기가 흐르면 자석의 성질을 띠는 전자석을 이용해서 ON/OFF의 상태가 변한다.
그러나 기계적인 움직임이 있기 때문에 속도는 빠르지 않았다.

진공관 (Elector Tube, Vaccum Tube)
더 발전된 자동장치는 진공관(Electron Tube, Vacuum Tube) 이다.
진공관은 1906년 개발되었고, 최초의 상업적인 진공관은 1920년 RCA에 의해 발명되었다.
기계적인 요소가 없기 때문에 작동하는 속도가 매우 빠르다.
진공관으로 이해 라디오, 텔레비전, 오디오, Telephone network, ENIAC 등이 탄생할 수 있었다.

Automata의 설계
Automata를 작동하는 원리는 아래 단계를 거쳐 설계된다.
- 원하는 기능을 문장으로 나열한다.
- 원하는 기능을 단위 명제로 나눈다.
- 나눠진 단위명제를 truth table로 나타낸다.
- Boolean expression을 이용하여 간단하게 만든다.
예를 들어, 댐 수문을 조절하는 자동장치를 만든다고 하자.
- 우리가 원하는 기능은 다음과 같다.
- 댐 수위가 높은데 비가 오면 수문을 연다.
- 또는 논에 물이 적으면 수문을 연다.
- 이를 단위명제로 나눈다.
- x : 댐의 수위가 높다.
- y : 비가 온다.
- z : 논에 물이 충분하다.
- F(Output) : 댐의 수문을 연다.
- 이를 truth table로 나타낸다.
- 아래 표 확인
- truth table을 boolean expression을 이용해 나타낸다.
- $F = x \cdot y + \bar {Z}$
- 이를 logic diagram으로 나타내면 아래 그림과 같다.

3. 구현 기술의 발전 : Transistors
Transistor
반도체 기술을 이용해 만들어지며, 얇은 실리콘판 위에 여러 기체를 붙여서 만들어진다.
1947년 Bell lab에서 개발되었고, 현재 tansistor을 이용하여 ALU, 프로세서, 컴퓨터 등을 만들고 있다.
* ALU : Arithmetic and Logic Unit (산술 논리 연산 장치)


'Computer Science > Computer Architecture' 카테고리의 다른 글
| Abstraction과 Software Design (0) | 2021.03.14 |
|---|---|
| Abstraction과 Hardware Design (0) | 2021.03.14 |
| Transistor와 반도체 제조 공정 (0) | 2021.03.14 |
| Digital Logic : Combinational Logic, Sequential Logic (0) | 2021.03.13 |
| Introduction : 도구, 기계, 컴퓨터 (0) | 2021.03.11 |





댓글