Transformation
Geometric transformation(기하 변환)이란 기하학적인 구조를 가진 집합을 one-to-one mapping을 통해 옮기는 것으로, 쉽게말해서 점들의 집합을 이동시키는 것이다.
Vector space S에 있는 임의의 input vector v을 S에서 T로 옮기는 것으로, 다음과 같이 나타낼 수 있다.
$S \rightarrow \{ T(v) | v \in S \}$
평행이동(translate), 회전(rotate), 확대/축소(scale), 전단(shear), 대칭(reflect) 등이 있다.
그래픽 movement, image/object manipulation, viewing, projection transform 등에 사용된다.
Linear Transformation
행렬곱(matrix multiplication)을 통해 transformation 하는 방법이다.
matrix multiplication은 linear mapping으로 나타낼 수 있기 때문에 linear transformation이라 한다.
$T(\textbf{v}) = M\textbf{v}$
$T(a\textbf{u} + \textbf{v}) = aT(\textbf{u}) + T(\textbf{v})$
$M\cdot (a\textbf{u} + \textbf{v}) = a\textbf{Mu} + \textbf{Mv}$
2D Linear Transformation
2x2 행렬이 2D linear transformation을 나타내며, 다음과 같은 transformation이 가능하다.
Translation의 경우 linear transformation이 아니다.
- scale
- uniform scale
- non-uniform scale
- rotation
- shear
- reflection
Scale
x축이나 y축 방향으로 늘리거나 줄이는 것이다.
x축과 y축을 같은 배율만큼 scale 하는 것을 uniform scale이라 하고, 다른 정도로 scale 하는 것을 non-uniform scale이라 한다.
다음과 같이 나타내고 $s_x$와 $s_y$가 같으면 uniform scale, 다르면 non-uniform scale이다.
$S = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}$
$\begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} s_xx \\ s_yy \end{bmatrix}$
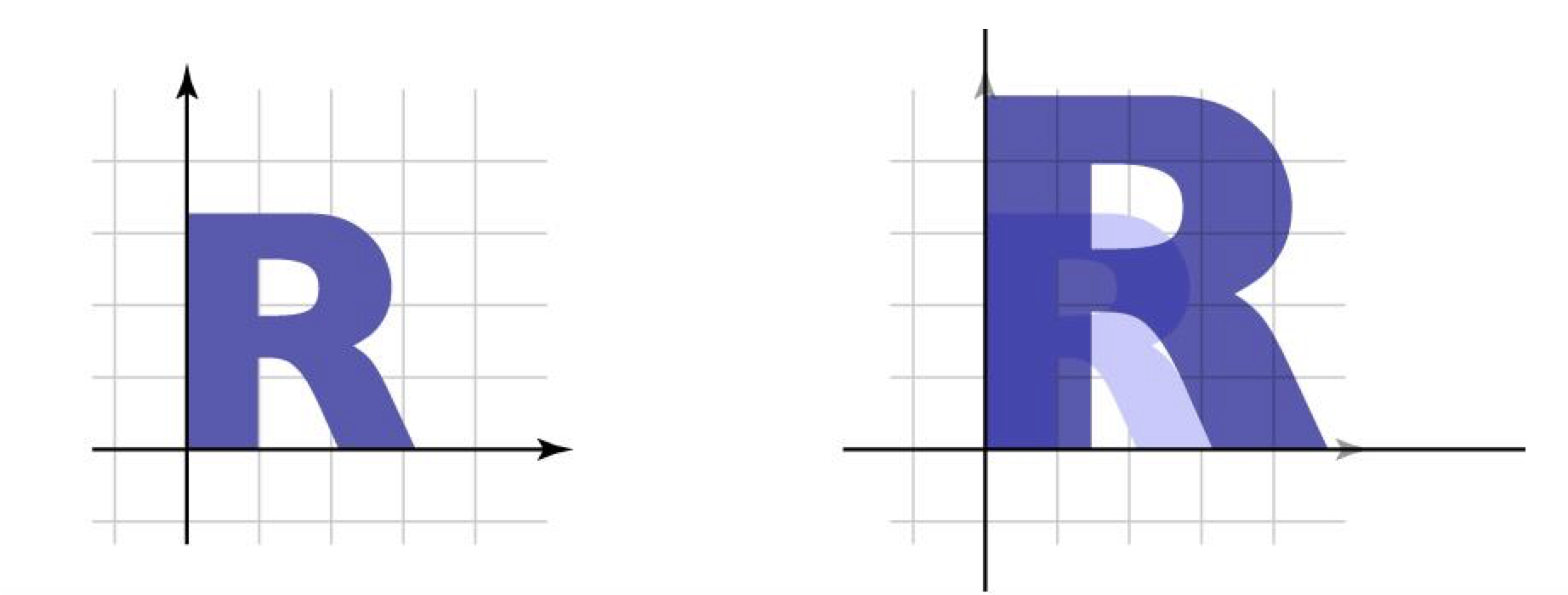
위 S matrix에서 각 column은 transformed된 좌표계에서의 basis vector(Canonical basis vector가 변형된 단위 벡터)이다.
Canonical basis vector란 cartesian coordinate system(좌표평면)에서의 축방향을 가리키고 있는 단위벡터이다.

Rotate
도형의 원점을 기준으로 $\theta\;radian$만큼 회전한 것으로 다음과 같이 나타낸다.
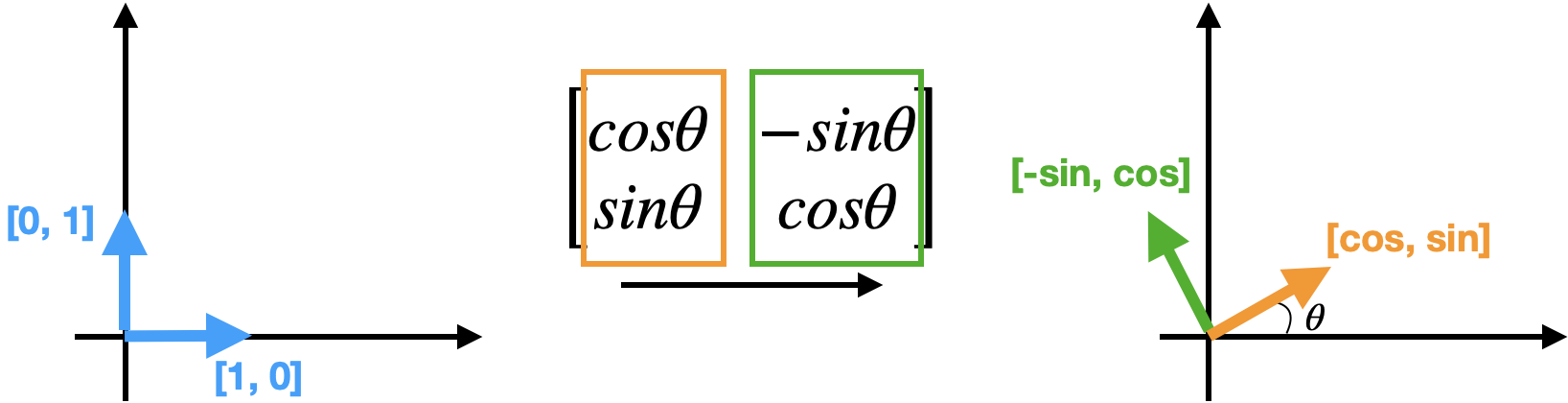
$R_\theta = \begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$
$\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} xcos\theta - ysin\theta \\ xsin\theta + ycos\theta \end{bmatrix}$
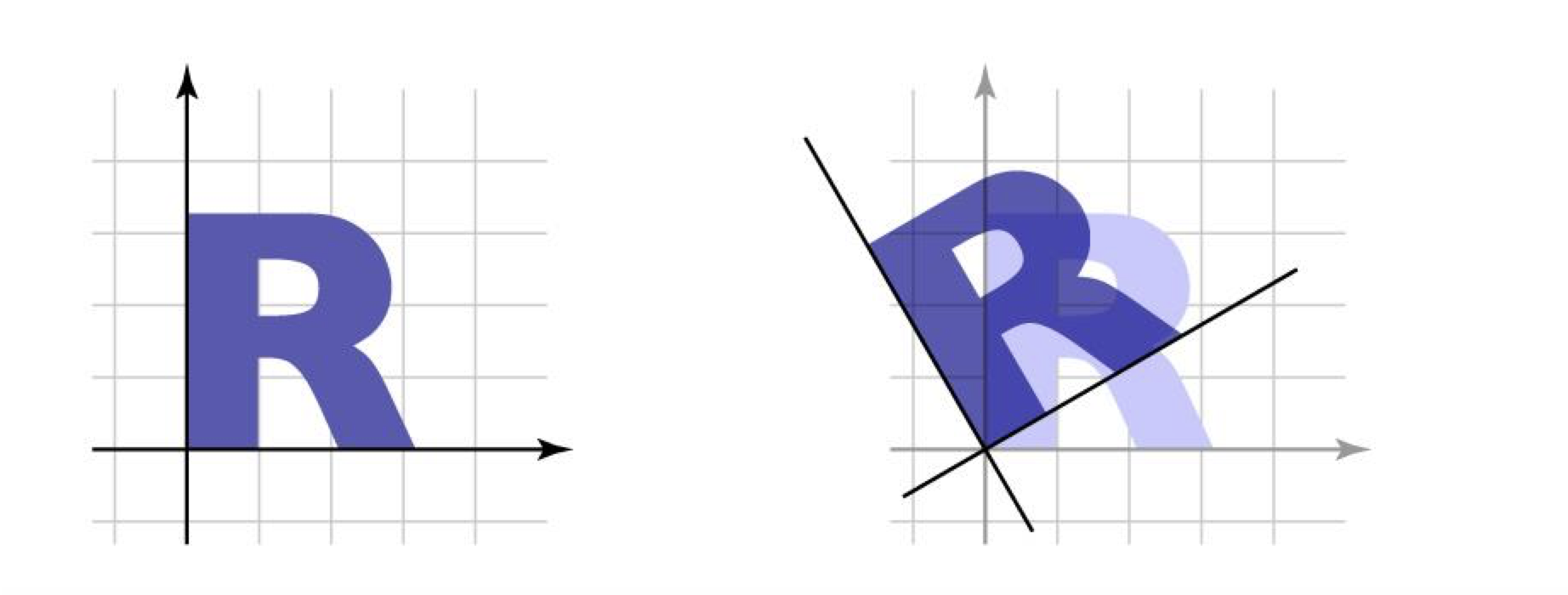
Column vector의 가능한 모든 linear comination의 집합을 column space of a matrix라 한다.
위 $R_\theta$에서의 각 column vector가 column space의 basis vector이다.
쉽게 회전된 축에서의 단위벡터이다.
Reflection
어떤 축을 기준으로 대칭(반사) 시킨 것으로 non-uniform scale의 한 케이스로 볼 수 있다.
세로(y) 축 대칭 : $\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}$
가로(x) 축 대칭 : $\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$

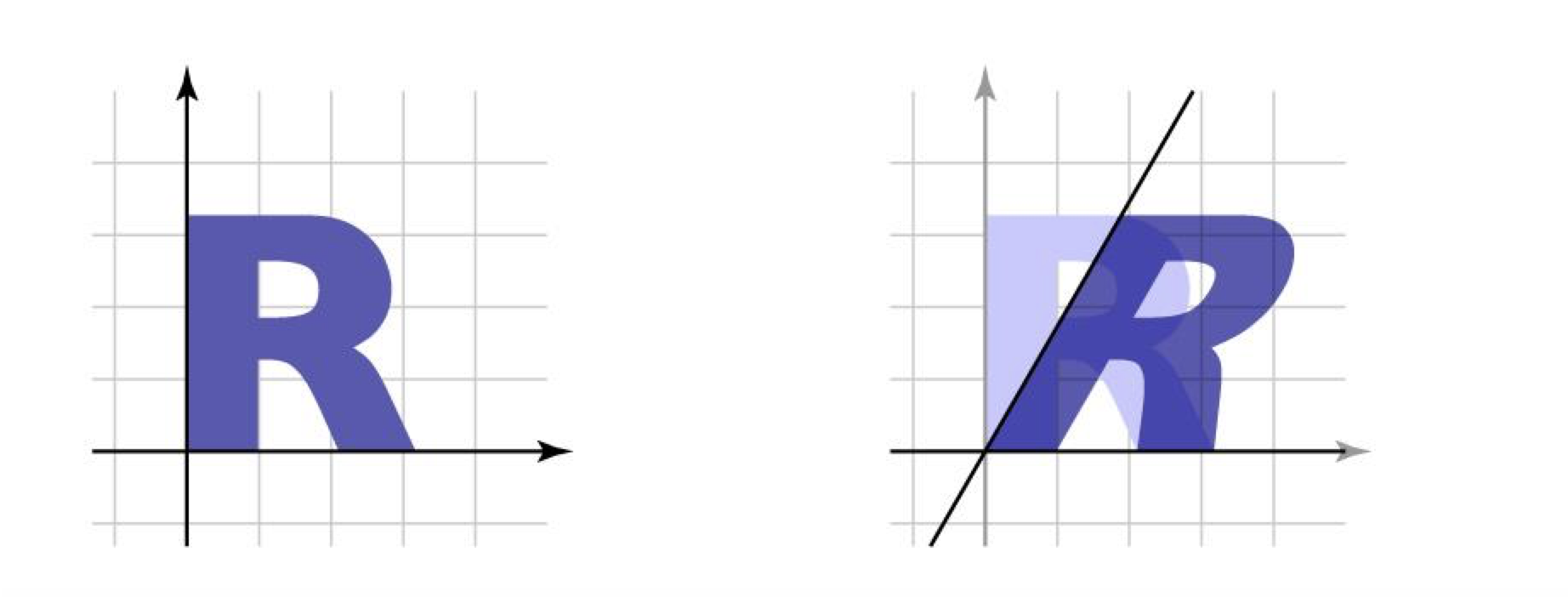
Shear
대각선으로 비틀린 모양으로 만든다.
좌우로 비틀기 : $\begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}$
위아래로 비틀기 : $\begin{bmatrix} 1 & 0 \\ a & 1 \end{bmatrix}$
Identity Matrix
아무런 변화를 일으키지 않는 행렬이다.
$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$
$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix}$
Affine Transformation
반(半, semi)선형 변환이다.
= linear transformation + translation
Linear transformation의 일부 특징을 포함해서 다음과 같은 특징을 가진다.
- preserve lines
- preserve parallel lines
- preserve ratios of distance along a line
2D Translation (평행이동)
2차원에서의 translation은 다음과 같이 일어난다.
$T(\textbf{v}) = \textbf{v} + \textbf{u}$
$T^{-1}(\textbf{v}) = \textbf{v} - \textbf{u}$
그런데 이는 matrix multiplation(행렬 곱)으로 나타낼 수 없으므로, linear transformation이 아니다.
이는 Affine transformation(반(半)선형 변환)에 속한다.
Rigid Transformation
Rotation + Translation으로, 회전과 평행이동을 동시에 수행한다.
$T(\textbf{v}) = R\textbf{v} + \textbf{u}$
다음과 같은 특징을 갖는다.
- preserve distances between all points
- preserve cross product for all vector => preserve angles
→ to avoid reflection
모든 vector끼리의 cross product(외적)이 유지된다. 이 덕분에 reflection을 피할 수 있게 된다.
만약 reflection을 통해 이동시키게되면 방향이 뒤집어져 되어버리기 때문에 cross product의 방향 또한 반대가 된다.
현재의 cross product가 화면 바깥쪽을 향하고 있다면 reflect하게 되면 cross product가 화면 안쪽을 향하게 되버린다.

Composing Transformations
여러 transformation 동작들을 수행할 수 있게 한다.
2D linear transformation은 2x2 matrix multiplication(행렬 곱)처럼 수행하면 된다.
다만, 실행 시에 뒤에서 앞 순서로 수행된다.
$\textbf{p} \rightarrow T(\textbf{p} \rightarrow S(T(\textbf{p})) = (S \circ T)(\textbf{p})$
순서의 중요
행렬 곱은 결합법칙은 성립하지만 교환법칙은 성립하지 않기 때문에 composing 할 때 순서가 중요하다.
아래는 축소 → 회전 순으로 composing하는 것과 회전 → 축소 순서로 composing 하는 것을 비교한 것이다.
두 개의 연산하는 matrix는 동일하지만 결과는 전혀 달라진다.

문제점
Linear transformation과 translation을 같이 composing 할 수 없다.
또한 affine transformation을 composing하는 것은 매우 복잡해진다.
→ 해결방법 : Homogeneous coordinates을 사용해서 composing하면 깔끔해진다.
Homogeneous Coordinates
2D points를 3D 좌표공간에 나타내서 연산을 수행한다.
Composing affine transformation도 3x3 matrix muliplication처럼 수행하면 된다.
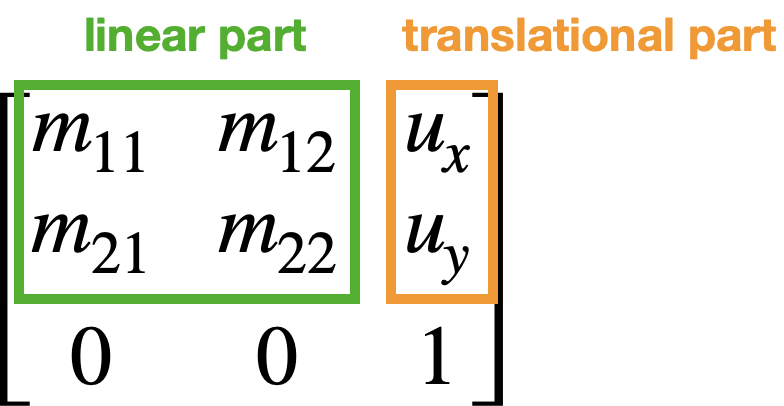
벡터를 위해서 extra component $w$가 추가되고, 2차원 matrix을 위해서는 extra row/column이 추가된다.
다만 좌표에 영향을 주지 않도록 추가되는 $w$는 1이 된다.
2차원의 좌표로 나타낼 수 있도록 결과값 중 주황색 박스를 사용한다.
예를 들어 <pre>M @ [:-1]</pre>과 같이 마지막 요소는 버리면 된다.

Translation

Affine transformation
참고
본 포스트는 한양대학교 이윤상 교수님의 수업을 정리한 내용입니다.
출처: 한양대학교 이윤상 교수님 컴퓨터그래픽스 강의 강의자료 - https://cgrhyu.github.io/courses/2022-spring-cg.html
CGR LAB
Computer Graphics - 2022 Spring Instructor: Yoonsang Lee Teaching Assistant: Chaejun Sohn Undergraduate Mentor: Bokyoung Jang Time / Location: Mon 09:00-11:00 / Online (originally 207 IT.BT Building) - Lab Wed 09:00-11:00 / 508 IT.BT Building - Lecture Cou
cgrhyu.github.io
'Computer Science > Computer Graphics' 카테고리의 다른 글
| [OpenGL] Transformation Matrix (0) | 2021.03.23 |
|---|---|
| Transformation in 3D (0) | 2021.03.16 |
| [GLFW] Input handling (0) | 2021.03.13 |
| [OpenGL] Vertex의 기본 (0) | 2021.03.12 |
| [OpenGL] OpenGL이란? (0) | 2021.03.10 |





댓글