Transformation in 3D

📝 목차

• 3D Cartesian Coordinate System

  • Right-handed vs Left-handed coordinates systems
  • 3x3 Matrix
• 3D Linear Transformation

  • Scale
  • Shear
  • Rotation
• Homogeneous Coordinate System in 3D

  • 참고 : 점의 표현 : 2D vs 3D
• Affine Transformation

  • Translation (평행이동)
  • Affine Transformation
• 참고

  • 'Computer Science > Computer Graphics' 카테고리의 다른 글

---

3D Cartesian Coordinate System

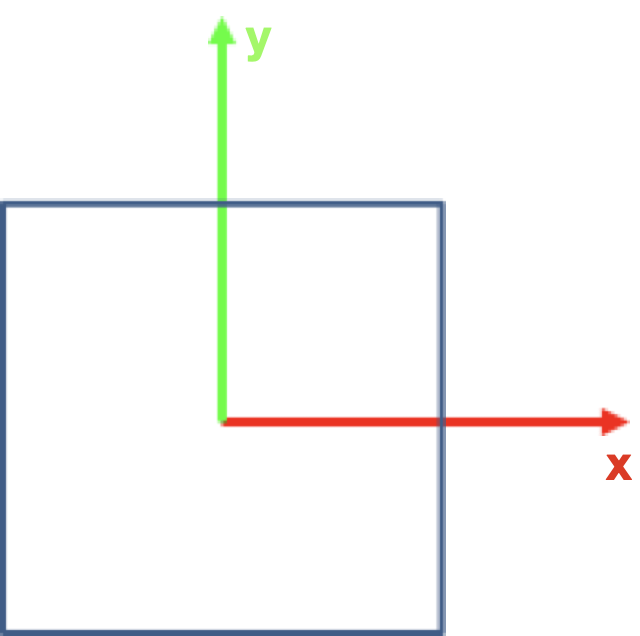
왼쪽은 2차원 좌표평면에서의 모습이고, 오른쪽은 3차원 좌표공간에서의 모습이다.

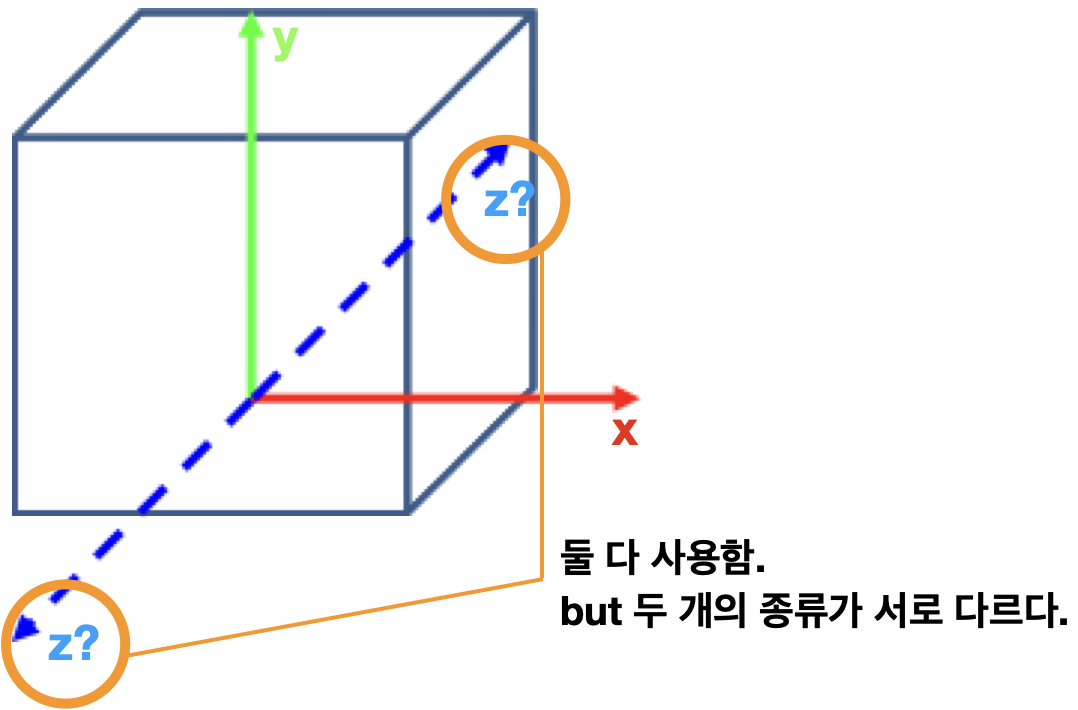
그런데 3차원의 경우 z축을 어디로 잡느냐를 결정해야 한다.

 

둘 다 사용하고 있으며 앞쪽으로 나와있는 것을 Right-handed cartesian coordinates라고 하고, 뒤쪽으로  빠져있는 것을 Left-handed cartesian coordinates라고 한다.

좌 : 2차원 / 우 : 3차원

 

Right-handed vs Left-handed coordinates systems

오른손을 폈을 때 손가락이 x축을 향하고 그 상태로 손가락을 접었을 때 y축을 향하게 두었을 때, z축이 엄지손가락 방향이면 Right-handed cartesian coordinates이다.

반면에 왼손으로 했을 때 엄지손가락이 z축을 향한다면 Left-handed cartesian coordinates이다.

Cartesian coordinate system in 3D

 

3x3 Matrix

Cartesian coordinates에서 3x3 matrix는 아래와 같이 나타낸다.

$\begin{bmatrix} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{bmatrix} \begin{bmatrix}p_x \\ p_y \\ p_z \end{bmatrix}$

 

---

3D Linear Transformation

2D에서 했던 것과 거의 같은 방식으로 진행된다.

다만, transformation되는 방향이 x, y축에서 x, y, z 축으로 변경되었다.

 

Scale

x, y, z축 방향으로 일정 배율 늘린다.

$S_s = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix}$

 

 

Shear

어떠한 축 방향으로 미는 것이다.

• y, z축은 그대로 두고, x 축 방향으로 밀 때,

$H_{x, d} = \begin{bmatrix} 1 & d_y & d_z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$

$\begin{bmatrix} 1 & d_y & d_z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x + y \cdot d_y + z \cdot d_z \\ y \\ z \end{bmatrix}$

 

 

• x, z축은 그대로 두고, y축 방향으로 밀 때,

$H_{y, d} = \begin{bmatrix} 1 & 0 & 0 \\ d_x & 1 & d_z \\ 0 & 0 & 1 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 & 0 \\ d_x & 1 & d_z \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x \\ x \cdot d_x + y + z \cdot d_z \\ z \end{bmatrix}$

 

• x, y축은 그대로 두고, z축 방향으로 밀 때,

$H_{z, d} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ d_x & d_y & 1 \end{bmatrix}$
$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ d_x & d_y & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x \\ y \\ x \cdot d_x + y \cdot d_y + z \cdot d_z \end{bmatrix}$

 

 

Rotation

어떠한 한 축을 기준으로 회전시킨다.

• x축을 기준으로 회전시켰을 때
  
  • x의 좌표는 변하지 않는다.

$R_{x, \theta} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\theta & -sin\theta \\ 0 & sin\theta & cos\theta \end{bmatrix}$

 

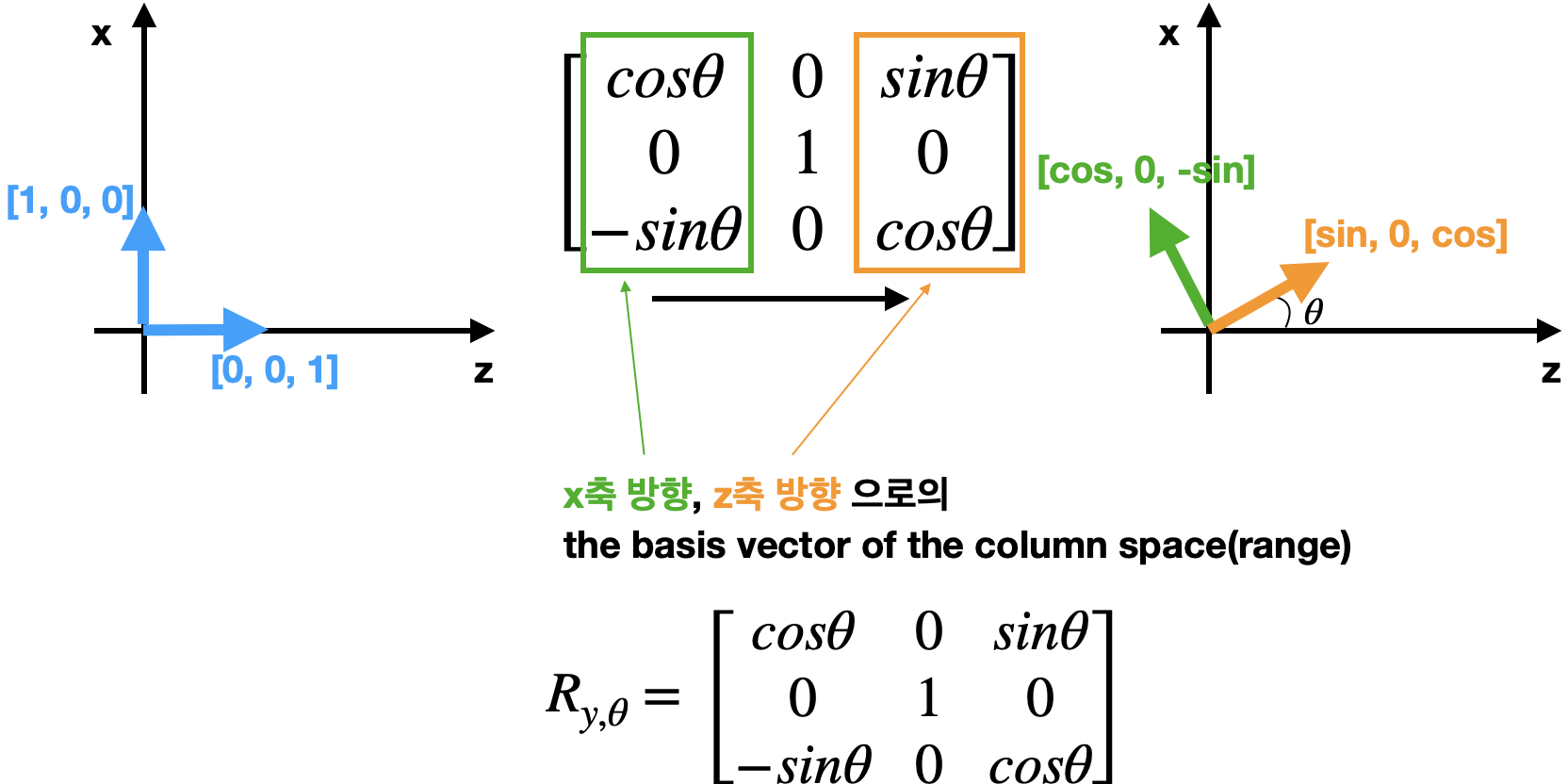
• y축을 기준으로 회전시켰을 때
  • y의 좌표는 변하지 않는다.
  • $sin$의 부호가 다름에 주의해야한다!

$R_{y, \theta} = \begin{bmatrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ -sin\theta & 0 & cos\theta \end{bmatrix}$

 

• z축을 기준으로 회전시켰을 때
  • z의 좌표는 변하지 않는다.

$R_{z, \theta} = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$

 

---

Homogeneous Coordinate System in 3D

Homogeneous coordinate는 기존의 차원에서 1인 point를 한개 더 추가한 것으로 matrix를 만든다.

즉, 3D에서는 아래와 같이 4개로 vector가 표현된다.

 

$[p_x, p_y, p_z, \textbf{1}]$

 

$\begin{bmatrix} m_{11} & m_{12} & m_{13} & 0 \\ m_{21} & m_{22} & m_{23} & 0 \\ m_{31} & m_{32} & m_{33} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}p_x \\ p_y \\ p_z \end{bmatrix}$

 

 

참고 : 점의 표현 : 2D vs 3D

 

---

Affine Transformation

Translation (평행이동)

Cartesian coordinates에서는 vector addition으로 나타난다.

$\begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} + \begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix}$

 

Homogeneous coordinates에서는 4x4 matrix multiplication으로 나타난다.

$\begin{bmatrix} 1 & 0 & 0 & u_x \\ 0 & 1 & 0 & u_y \\ 0 & 0 & 1 & u_z \\ 0 & 0 & 0 & 1 \end{bmatrix}$

 

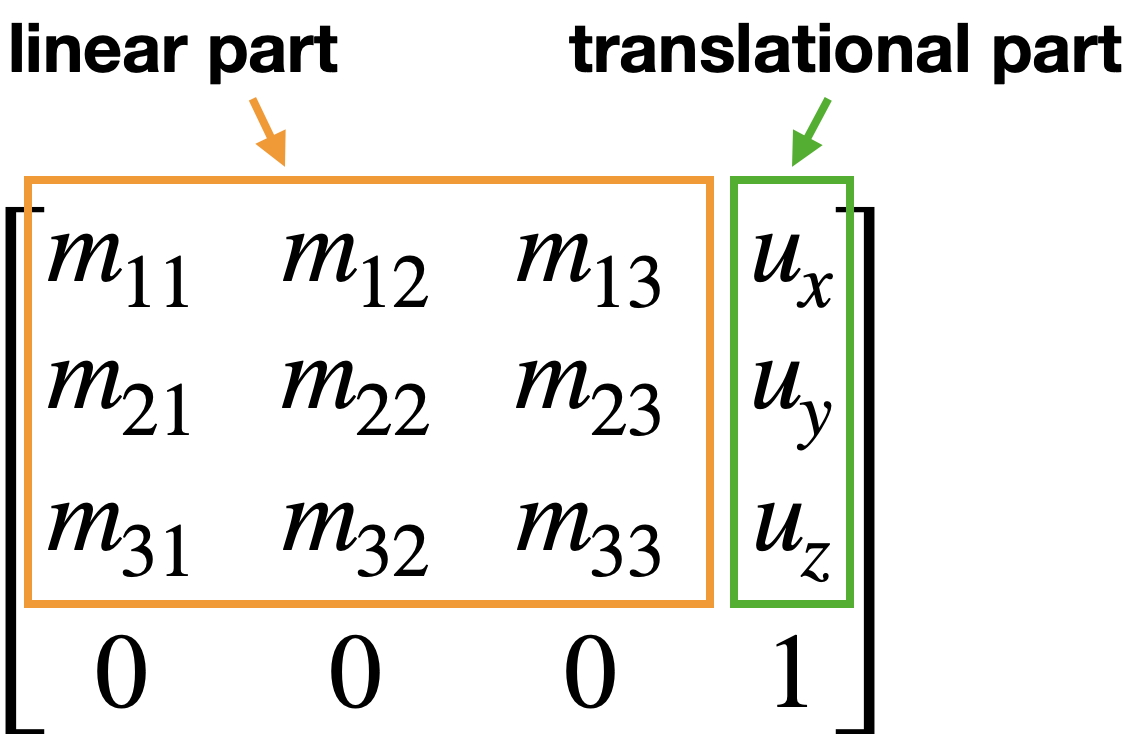
Affine Transformation

Homogeneous coordinates에서 Affine transformation은 4x4 matrix로 표현된다.

2D에서와 유사한 모습이다.

 

---

참고

본 포스트는 한양대학교 이윤상 교수님의 수업을 정리한 내용입니다.

출처: 한양대학교 이윤상 교수님 컴퓨터그래픽스 강의 강의자료 - https://cgrhyu.github.io/courses/2022-spring-cg.html

CGR LAB