Kinematics
물체들의 움직임에 대한 연구 분야이다.
질량(mass), 힘(force) 등의 물리적인 요소는 고려하지 않고, 움직임 자체에 대해서만 다룬다.
컴퓨터 그래픽스에서 여러개의 관절로 이루어진 다관절체(skeleton)를 움직일 때 사용된다.
- Forward kinematics
- $(p, q) \, = \, F( \theta_i )$
- 관절(joint)의 angle을 이용하여 end-effector의 position, orientation을 계산한다.
- approach가 명확히 정의되어있으며, 계산도 비교적 간단하다.
- Inverse kinematics
- $\theta_i \, = \, F^{-1} (p, q)$
- end-effector의 position, orientation을 이용하여 joint의 각도를 구하는 것이다.
- approach가 0개, 1개, 여러개, 무한개 일 수도 있다.

Dynamics (Kinetics)
Kinematics와 대조되는 학문으로, 움직임과 움직임을 만들어내는 원인(mass, force 등)의 관계에 대한 연구 분야이다.
Forward Kinematics
삼각함수를 이용하여 위치를 구할수도 있지만, transformation matrix을 이용할 수도 있다.
삼각함수 이용
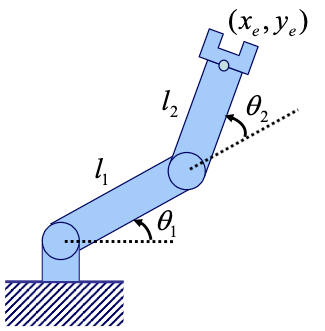
아래 그림에서 $(x, y)$의 좌표는 삼각함수를 이용하여 다음과 같이 구할 수 있다.
$x_e = l_1 cos\theta_1 \, + \, l_2 cos( \theta_1 + \theta_2 )$
$y_e = l_1 sin \theta_1 + l_2 sin( \theta_1 + \theta_2 )$
Transformation matrix 이용
아래에서 T를 구하는 과정으로 생각하면, 다음과 같다.
Matrix T를 forward kinematics map이라 한다.



Forward Kinematics Map
Joint value를 end-effector의 postion과 orientation으로 mapping하는 과정을 말한다.
Matrix T를 구하는 과정이라고 생각할 수 있다.
Forward kinematics map은 여러 개의 joint transformation과 link transformation이 교차하면서 곱해진다.
- Joint transformation
- joint의 movement를 나타낸다.
- 시간에 따라서 변하는 움직임이다. (time-varying)
- 관절의 위치는 시간이 지남에 따라 변한다.
- 주로 rotation이다.
- Link transformation
- parent에 상대적인 frame이다.
- static한 움직임이다. (시간에 따라 변하지 않는다.)
- parent와의 관계는 시간이 지나도 변하지 않는다.
- 주로 translation이다.
발 끝(end-effector)의 frame은 $T \, (0, 0, 0, 1)^T$ 로 표현할 수 있다.
$J_0$는 root가 global frame으로부터 얼마만큼 rotate하고 얼마만큼 translate 했는지를 나타낸다.
Root는 translate + rotate(rigid)이기 때문에 6 자유도(DOF)를 가진다.
각각의 $J_1, L_1, J_2, L_2 ...$은 3 자유도를 갖는다.
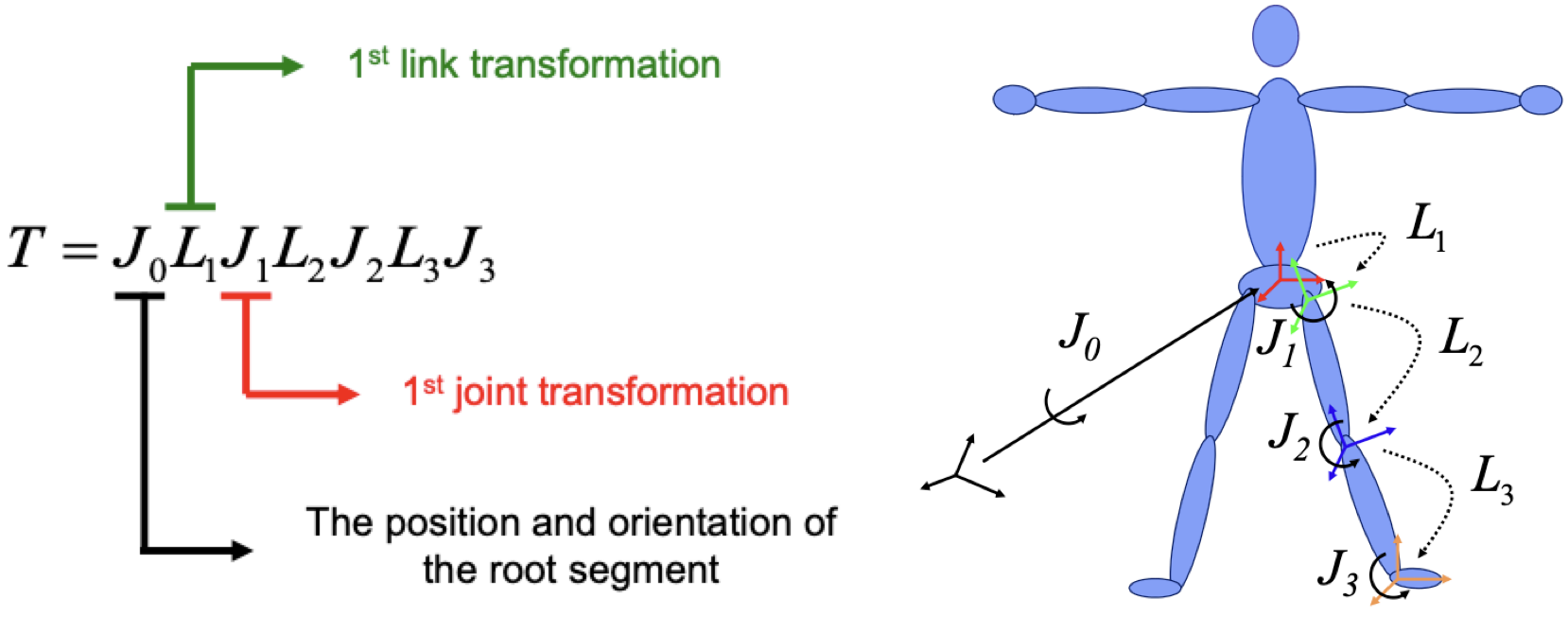
참고
본 포스트는 한양대학교 이윤상 교수님의 수업을 정리한 내용입니다.
출처: 한양대학교 이윤상 교수님 컴퓨터그래픽스 강의 강의자료 - https://cgrhyu.github.io/courses/2022-spring-cg.html
CGR LAB
Computer Graphics - 2022 Spring Instructor: Yoonsang Lee Teaching Assistant: Chaejun Sohn Undergraduate Mentor: Bokyoung Jang Time / Location: Mon 09:00-11:00 / Online (originally 207 IT.BT Building) - Lab Wed 09:00-11:00 / 508 IT.BT Building - Lecture Cou
cgrhyu.github.io
'Computer Science > Computer Graphics' 카테고리의 다른 글
| Curve, Spline (1) | 2021.06.01 |
|---|---|
| Character Animation, BVH Format (6) | 2021.06.01 |
| 3D Orientation Interpolation (0) | 2021.06.01 |
| Orientation, Rotation (0) | 2021.06.01 |
| Hierarchical Modeling (0) | 2021.05.31 |





댓글