Degrees of Freedom (DOF, 자유도)
"몇개의 숫자로 움직임(상태)를 표현할 수 있는가"를 말한다.
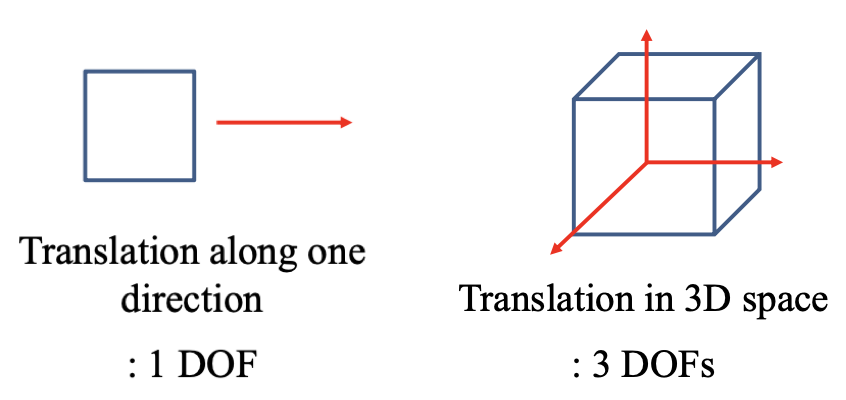
예를 들어, 직선에서의 translation은 -1, +5 등 숫자 1개로 표현할 수 있으므로 1DOF를 가진다.
반면, 3차원에서의 translation은 x, y, z 축에 대한 거리를 표현해야 하므로 3DOF를 가진다.
Orientation & Rotation
- Orientation
- ≒ point, state
- 상태
- state of being oriented
- coordinate system에서의 orientation은 origin으로부터의 rotation으로 표현될 수 있다.
- Rotation
- ≒ vector, movement
- 움직임
- circular movement
관계
orientation : vector의 관계는
= point : vector
= state : movement
의 관계와 유사하다.
point/vector와 마찬가지로 homogeneous coordinate에 부합한다.
따라서 연산의 결과는 다음과 같다.
- orientation + orientation → undefined
- rotation ± rotation → rotation
- orientation ± rotation → orientation
- orientation - orientation → rotation
3D Orientation & Rotation
하나의 orientation에서 다른 orientation으로 가는 어떠한 rotation도 항상 하나의 회전축과 각도로 표현이 가능하다.

Euler's Rotation Theorem
Rigid body란 크기나 모양이 변화되지 않는 물체(translation + rotation)이다.
이에 대해 다음과 같은 내용이 적용된다.
- Rigid body의 한 점이 고정된 움직임은 어떤 축에 대한 rotation으로 표현이 가능하다.
- 임의의 회전은 어떤 한 축에 대한 회전이다.
- 어떤 회전이더라도 한 vector는 변하지 않고 그대로 남아있다.
- 남아있는 vector가 회전축 vector이다.
Rotation과 Orientation을 표현하는 방법
다음과 같은 방법을 이용해서 3차원 공간에서의 회전을 표현한다.
- Euler angle
- 3 parameter
- Rotation vector (Axis-angle)
- 3 parameter
- Rotation matrices
- 9 parameter
- Unit quaternions
- 4 parameter
각 표현의 문제점
Euler angle과 rotation vector는 3개의 parameter를 사용하기 때문에 다음과 같은 문제점이 생긴다.
- Euler angle
- discontinuity (or many-to-one correspondence)
- gimbal lock
- Rotation vector
- discontinuity (or many-to-one correspondence)
이를 해결하기 위해서 DOF 보다 더 많은 수의 parameter를 사용해야 한다.
* 3차원에서의 회전은 3DOF이다.
- Rotation matrices : 9 parameter
- Unit quaternions : 4 parameter
Conversion
- Rotation vector → Rotation matrix
- Rodrigues' rotation fomula (log())
- Rotatio matrix → Rotation vector
- exp() 이용
- Euler angle → Rotation matrix
- canonical rotation matrix를 composing
- 예 : Rx @ Ry @ Rz
Euler Angle
임의의 3차원 회전을 3개의 축에 대해서 3개의 rotation angle로 표현하는 방법이다.
조합
여러 축에 대한 조합이 가능하다.
- 같은 축이 연속되지 않고 반복되도 괜찮다.
- 다만, XXY와 같이 연속으로 같은 축에 대해서 회전하는 것은 결국 XY와 같으므로 안된다.
- 다음과 같이 12개의 조합이 가능하다.
- XYZ, XYX, XZY, XZX
- YZX, YZY, YXZ, YXY
- ZXY, ZXZ, ZYX, ZYZ
회전
각 축에 대한 회전은 rotation matrix를 이용하면 된다.

예를 들어, ZXZ Euler angle은
- z축에 대해서 회전하고
- x축에 대해서 회전하고
- z축에 대해서 회전한다.

만약 ZXY Euler angle이라면, Rz() Rx() Ry()의 순으로 matrix를 곱하면 된다.
문제점
3개의 parameter로 표현(3DOF)하기 때문에 다음과 같은 문제가 발생한다.
- discontinuity (or many-to-one correspondences)
- gimbal lock
Discontinuity (or many-to-one correspondences)
motion은 continuous하지만, 그 표현은 discontinuous 할 수 있다.
각도가 $-\pi$ ~ $\pi$ 까지만 가질 수 있기 때문에 도중에 discontinuous 해진다.
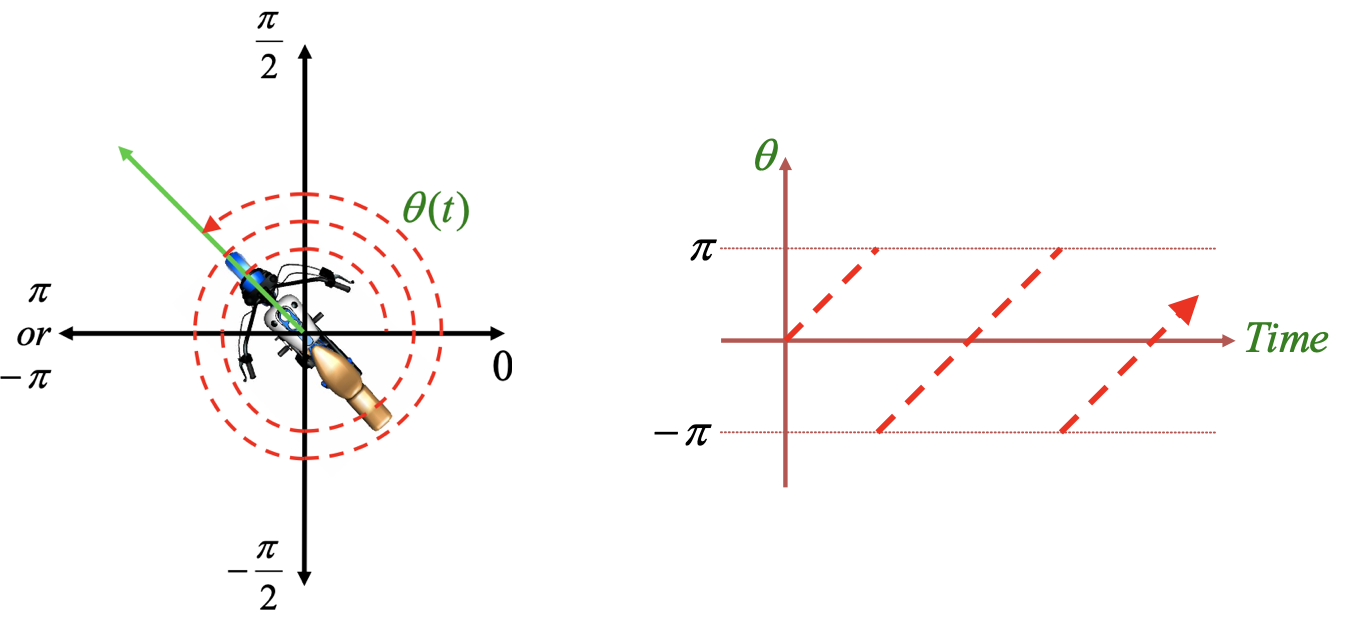
만약 discontinuous하지 않게 연속적으로 나타낸다면 이제는 many-to-one correspondences 문제를 가지게 된다.
동일한 motion이지만, representation은 여러 개 나오는 것이다.

Gimbal Lock
두개의 축이 같아지는 순간에 gimbal lock이 발생한다.
Gimbal lock이 발생하면 하나의 자유도를 잃게된다.
이에 따라 특정 방향으로는 움직이지 못한다.

의미
위와 같은 문제를 가지긴 하지만, 현실에서 Euler angle을 사용할 수 밖에 없는 경우가 있다.
3 자유도를 갖는 rotational joint를 만들기 위해서는 3개의 모터를 사용하기 때문이다.
그렇기에 Euler angle는 의미를 지닌다.
Rotation Vector (Axis-Angle)
회전축과 회전 각도를 vector로 나타낸 것이다.
$v = \theta, \hat{v} = (x, y, z)$
vector의 방향 : 회전축
vector의 길이 : 회전각
문제점
3개의 parameter로 표현(3DOF)하기 때문에 아래 문제가 발생한다.
- Discontinuity (or many-to-one correspondence)
Rotation Matrices
의미
Rotation matrix는 다음을 정의한다.
- rotate된 frame의 orientation
- global frame에서 rotate된 frame까지의 rotation

조건
아래 두 가지 조건을 만족하는 것을 rotation matrix라 한다.
- $R R^T = R^T R = I$
- $det(R) = 1$
- determinant : $ad-bc$
즉, rotation matrix는 determinant가 1인 orthogonal matrix이다.
3차원 공간상의 rotation matrix는 3x3이므로, special orthogonal group SO(3)라고도 한다.
특징
- $R^T$는 $R$의 inverse rotation이다.
- $R^{-1} = R^T$
- $R_1 R_2$도 rotation matrix이다.
- $(R_1 R_2)^T (R_1 R_2) = R_2 ^T R_1 ^T R_1 R_2 = I$
- $det(R_1 R_2) = det(R_1) \cdot det(R_2) = 1$
- vector $v$의 길이는 rotation을 해도 변하지 않는다.
- $\| Rv \| ^2 = (Rv)^T (Rv) = v^T R^T R v = v^T v = \| v \| ^2$
임의의 축에 대한 Rotation 계산
Rodrigues' rotation formula를 사용한다.
결국 rotation vector를 rotation matrix로 바꾸는 방법이다.
Normalized axis vector $u = (u_x, u_y, u_z)$에 대해 $\theta$ 만큼 회전하는 matrix는 다음과 같다.
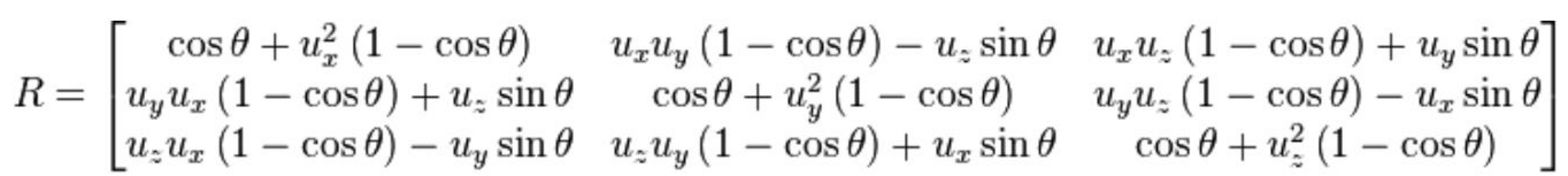
Unit Quaternions
Quaternion
복소수를 3차원으로 확장한 개념이다.
$q = w + ix + jy + kz$
$i^2 = j^2 = k^2 = ijk = -1$
$ij = k, \; jk = i, \;, ki = j$
$ji = -k, \; kj = -i , \; ik = -j$
Unit Quaternions
$q = w + ix + jy + kz$
$= (w, x, y, z)$
$= (w, v)$
단, $w^2 + x^2 + y^2 + z^2 = 1$
회전 축 $\hat{v}$에 대해 $\theta$ 만큼 회전하는 것은
$q = ( cos \frac{\theta} {2} , \hat{v} sin \frac {\theta} {2} )$
로 표현할 수 있다.
어떤 vector를 unit quaternion으로 회전시키는 것은
${p}' = qpq^{-1}$ ($p = (0, x, y, z)$)
가 된다.

Rotation Matrix vs. Unit Quaternion
공통점
- Rotation matrices와 unit quaternion은 표현력이 동일하다.
- 숫자를 많이 사용하기 때문에 redundant의 문제가 있지만, signularity가 없다.
- axis-angle representation으로 표현될 수 있다.
Rotation Matrix의 장점
- one-to-one correspondence이다.
- unit quaternion은 하나의 orientation을 의미하는 quaternion이 두 개 존재한다. (q = -q)
- rotation과 translation을 동일한 방법으로 처리할 수 있다.
- 4x4 homogeneous matrices 사용
Unit Quaternion의 장점
- 더 적은 수의 parameter를 사용한다.
- 계산이 간단하다.
- numerical error를 보정하기 더 쉽다.
참고
본 포스트는 한양대학교 이윤상 교수님의 수업을 정리한 내용입니다.
출처: 한양대학교 이윤상 교수님 컴퓨터그래픽스 강의 강의자료 - https://cgrhyu.github.io/courses/2022-spring-cg.html
CGR LAB
Computer Graphics - 2022 Spring Instructor: Yoonsang Lee Teaching Assistant: Chaejun Sohn Undergraduate Mentor: Bokyoung Jang Time / Location: Mon 09:00-11:00 / Online (originally 207 IT.BT Building) - Lab Wed 09:00-11:00 / 508 IT.BT Building - Lecture Cou
cgrhyu.github.io
'Computer Science > Computer Graphics' 카테고리의 다른 글
| Kinematics (0) | 2021.06.01 |
|---|---|
| 3D Orientation Interpolation (0) | 2021.06.01 |
| Hierarchical Modeling (0) | 2021.05.31 |
| Affine Transformation Matrix, Transformation의 해석 (0) | 2021.05.31 |
| [OpenGL] Lighting, Shading (0) | 2021.05.31 |





댓글