Interpolation
알려진 데이터를 이용해서 새로운 데이터를 추론하는 것이다.
- nearest-neighbor : 주변의 데이터를 이용
- linear : 알려진 데이터를 선으로 연결해서 추론
- polynomial : 알려진 데이터를 다항식을 이용해서 연결
- spline : 다항식을 여러 조각을 연결

Linear Interpolation
일반적인 경우
내분한다고 생각하면 간단하다.


정확하지 않은 방법
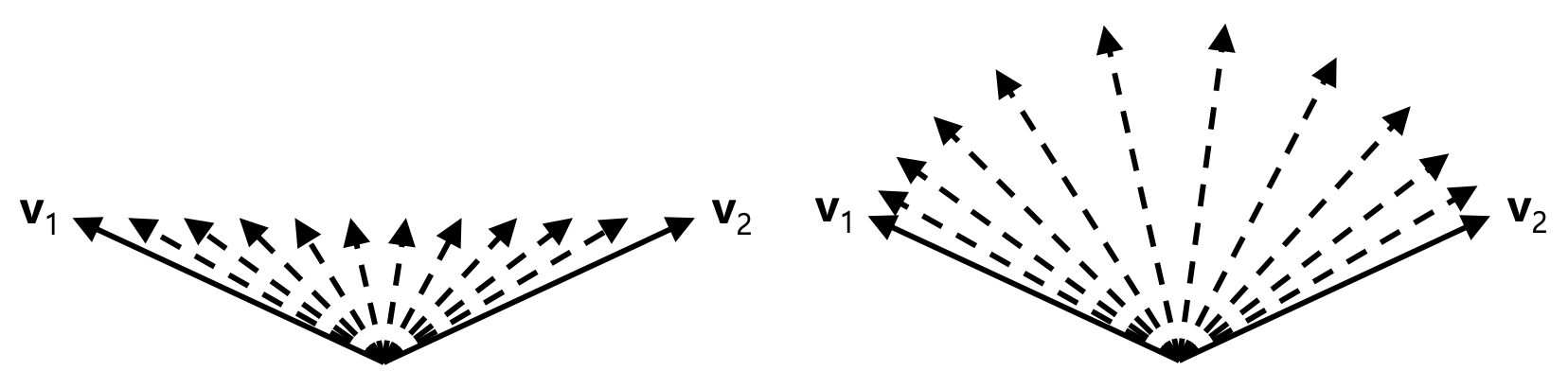
각 element마다 linear interpolation을 적용하면 정확하지 않은 결과를 얻게된다.
- Euler angle
- Rotation vector
- Rotation matrices

- Unit quaternions
Slerp
Spherical Linear Interpolation
정확한 결과를 얻기 위해서는 slerp을 해야 한다.
두 개의 orientation 사이의 linear interpolation을 구할 수 있게 해준다.
$slerp(R_1, R_2, t) = R_1 ( R_1 ^T R_2 )^t$
$= R_1 exp(t \cdot log( R_1 ^T R_2 ))$
exp() : rotation vector → rotation matrix
log() : rotation matirx → rotation vector
$R^t$의 의미는 rotation angle을 scaling 하는 것이다.
exp()
rotation vector → rotation matrix
Rodrigues' rotation formula 를 이용한다.
회전축 $u = (u_x, u_y, u_z)$에 대해 $\theta$ 만큼 rotate하면,
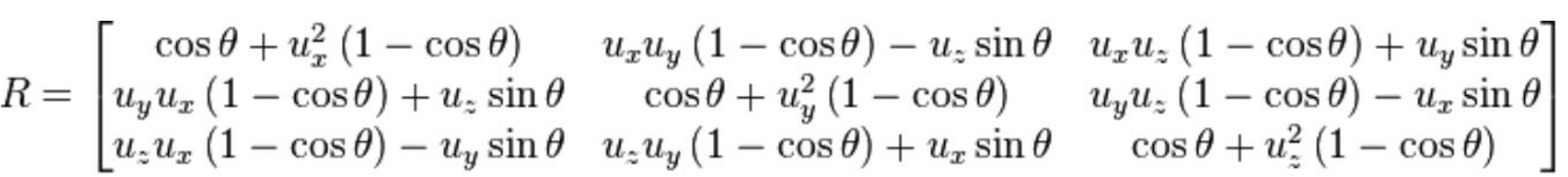
log()
아래를 이용해서 rotation matrix → rotation vector를 수행한다.
단, $sin \theta$가 0면 나눌 수 없으므로 singularity가 존재한다.


참고
본 포스트는 한양대학교 이윤상 교수님의 수업을 정리한 내용입니다.
출처: 한양대학교 이윤상 교수님 컴퓨터그래픽스 강의 강의자료 - https://cgrhyu.github.io/courses/2022-spring-cg.html
CGR LAB
Computer Graphics - 2022 Spring Instructor: Yoonsang Lee Teaching Assistant: Chaejun Sohn Undergraduate Mentor: Bokyoung Jang Time / Location: Mon 09:00-11:00 / Online (originally 207 IT.BT Building) - Lab Wed 09:00-11:00 / 508 IT.BT Building - Lecture Cou
cgrhyu.github.io
'Computer Science > Computer Graphics' 카테고리의 다른 글
| Character Animation, BVH Format (6) | 2021.06.01 |
|---|---|
| Kinematics (0) | 2021.06.01 |
| Orientation, Rotation (0) | 2021.06.01 |
| Hierarchical Modeling (0) | 2021.05.31 |
| Affine Transformation Matrix, Transformation의 해석 (0) | 2021.05.31 |





댓글